Proportional Topology Optimization algorithm with virtual elements for multi-material problems considering mass and cost constraints
Author affiliations
DOI:
https://doi.org/10.15625/0866-7136/19613Keywords:
linear virtual element method, proportional topology optimization, ordered SIMP, multi-materialAbstract
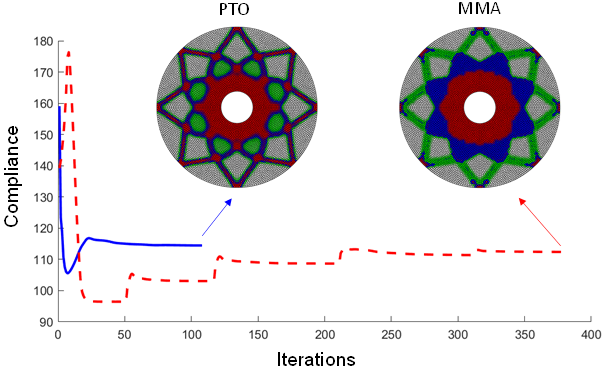
This paper presents an extension of the Proportional Topology Optimization (PTO) with virtual elements for multi-material problems with mass and cost constraints. In particular, the linear virtual element method (VEM) is constructed on unstructured polygonal meshes. The linear VEM is desirable in the sense that numerical integration is not explicitly required, significantly reducing the computational effort. Furthermore, the unstructured polygonal mesh naturally eliminates the issue of one-node connections encountered by the usual quadrilateral mesh. A feature of PTO is that it does not require sensitivity information, i.e., the derivative of the objective function with respect to design variables. Instead, the amount of material distributed into each element is determined proportionally to the contribution of that element to the objective function. For multi-material problems, the Ordered Solid Isotropic Material with Penalization (Ordered SIMP) technique is integrated into the PTO framework. Compared to other techniques for problems that involve multiple materials, Ordered SIMP has the advantage that computational cost does not depend on the number of materials. Furthermore, for the first time, the PTO approach is extended to consider two types of constraints: mass and cost simultaneously. The feasibility and efficiency of the proposed method are demonstrated via several benchmark examples and comparisons with the existing approach.
Downloads
Metrics
References
M. P. Bendsoe and N. Kikuchi. Generating optimal topologies in structural design using a homogenization method. Computer Methods in Applied Mechanics and Engineering, 71, (1988), pp. 197–224. DOI: https://doi.org/10.1016/0045-7825(88)90086-2
M. P. Bendsoe. Optimal shape design as a material distribution problem. Structural Optimization, 1, (4), (1989), pp. 193–202. DOI: https://doi.org/10.1007/BF01650949
O. Sigmund. A 99-line topology optimization code written in Matlab. Structural and Multidisciplinary Optimization, 21, (2), (2001), pp. 120–127. DOI: https://doi.org/10.1007/s001580050176
M. Stolpe and K. Svanberg. An alternative interpolation scheme for minimum compliance topology optimization. Structural and Multidisciplinary Optimization, 22, (2), (2001), pp. 116–124. DOI: https://doi.org/10.1007/s001580100129
M. Y. Wang, X. Wang, and D. Guo. A level set method for structural topology optimization. Computer Methods in Applied Mechanics and Engineering, 192, (1-2), (2003), pp. 227–246. DOI: https://doi.org/10.1016/S0045-7825(02)00559-5
V. J. Challis. A discrete level-set topology optimization code written in Matlab. Structural and Multidisciplinary Optimization, 41, (3), (2009), pp. 453–464. DOI: https://doi.org/10.1007/s00158-009-0430-0
P. Wei, Z. Li, X. Li, and M. Y. Wang. An 88-line MATLAB code for the parameterized level set method based topology optimization using radial basis functions. Structural and Multidisciplinary Optimization, 58, (2), (2018), pp. 831–849. DOI: https://doi.org/10.1007/s00158-018-1904-8
A. Takezawa, S. Nishiwaki, and M. Kitamura. Shape and topology optimization based on the phase field method and sensitivity analysis. Journal of Computational Physics, 229, (7), (2010), pp. 2697–2718. DOI: https://doi.org/10.1016/j.jcp.2009.12.017
L. Dede, M. J. Borden, and T. J. R. Hughes. Isogeometric analysis for topology optimization with a phase field model. Archives of Computational Methods in Engineering, 19, (3), (2012), pp. 427–465. DOI: https://doi.org/10.1007/s11831-012-9075-z
W. Zhang, J. Yuan, J. Zhang, and X. Guo. A new topology optimization approach based on Moving Morphable Components (MMC) and the ersatz material model. Structural and Multidisciplinary Optimization, 53, (6), (2015), pp. 1243–1260. DOI: https://doi.org/10.1007/s00158-015-1372-3
W. Zhang, D. Li, J. Zhou, Z. Du, B. Li, and X. Guo. A Moving Morphable Void (MMV)-based explicit approach for topology optimization considering stress constraints. Computer Methods in Applied Mechanics and Engineering, 334, (2018), pp. 381–413. DOI: https://doi.org/10.1016/j.cma.2018.01.050
J. A. Norato, B. K. Bell, and D. A. Tortorelli. A geometry projection method for continuumbased topology optimization with discrete elements. Computer Methods in Applied Mechanics and Engineering, 293, (2015), pp. 306–327. DOI: https://doi.org/10.1016/j.cma.2015.05.005
H. Smith and J. Norato. A MATLAB code for topology optimization using the geometry projection method. Structural and Multidisciplinary Optimization, 62, (3), (2020), pp. 1579–1594. DOI: https://doi.org/10.1007/s00158-020-02552-0
C. F. Hvejsel and E. Lund. Material interpolation schemes for unified topology and multimaterial optimization. Structural and Multidisciplinary Optimization, 43, (6), (2011), pp. 811–825. DOI: https://doi.org/10.1007/s00158-011-0625-z
D. Li and I. Y. Kim. Multi-material topology optimization for practical lightweight design. Structural and Multidisciplinary Optimization, 58, (3), (2018), pp. 1081–1094. DOI: https://doi.org/10.1007/s00158-018-1953-z
M. Y. Wang and X. Wang. “Color” level sets: a multi-phase method for structural topology optimization with multiple materials. Computer Methods in Applied Mechanics and Engineering, 193, (6-8), (2004), pp. 469–496. DOI: https://doi.org/10.1016/j.cma.2003.10.008
Y. Wang, Z. Luo, Z. Kang, and N. Zhang. Amulti-material level set-based topology and shape optimization method. Computer Methods in Applied Mechanics and Engineering, 283, (2015), pp. 1570–1586. DOI: https://doi.org/10.1016/j.cma.2014.11.002
S. Zhou and M. Y. Wang. Multimaterial structural topology optimization with a generalized Cahn-Hilliard model of multiphase transition. Structural and Multidisciplinary Optimization, 33, (2), (2006), pp. 89–111. DOI: https://doi.org/10.1007/s00158-006-0035-9
R. Tavakoli and S. M. Mohseni. Alternating active-phase algorithm for multimaterial topology optimization problems: a 115-line MATLAB implementation. Structural and Multidisciplinary Optimization, 49, (4), (2014), pp. 621–642. DOI: https://doi.org/10.1007/s00158-013-0999-1
K. N. Chau, K. N. Chau, T. Ngo, K. Hackl, and H. Nguyen-Xuan. A polytreebased adaptive polygonal finite element method for multi-material topology optimization. Computer Methods in Applied Mechanics and Engineering, 332, (2018), pp. 712–739. DOI: https://doi.org/10.1016/j.cma.2017.07.035
J. Park, T. H. Nguyen, J. J. Shah, and A. Sutradhar. Conceptual design of efficient heat conductors using multi-material topology optimization. Engineering Optimization, 51, (5), (2018), pp. 796–814. DOI: https://doi.org/10.1080/0305215X.2018.1497613
M. N. Nguyen and T. Q. Bui. Multi-material gradient-free proportional topology optimization analysis for plates with variable thickness. Structural and Multidisciplinary Optimization, 65, (2022). DOI: https://doi.org/10.1007/s00158-022-03176-2
W. Sha, M. Xiao, L. Gao, and Y. Zhang. A new level set based multi-material topology optimization method using alternating active-phase algorithm. Computer Methods in Applied Mechanics and Engineering, 377, (2021). DOI: https://doi.org/10.1016/j.cma.2021.113674
A. Habibian and Sohouli. Multi-material topology optimization of structures with discontinuities using Peridynamics. Composite Structures, 258, (2021). DOI: https://doi.org/10.1016/j.compstruct.2020.113345
Z. Han, K. Wei, Z. Gu, X. Ma, and X. Yang. Stress-constrained multi-material topology optimization via an improved alternating active-phase algorithm. Engineering Optimization, 54, (2), (2021), pp. 305–328. DOI: https://doi.org/10.1080/0305215X.2020.1867119
M. N. Nguyen, M. T. Tran, H. Q. Nguyen, and T. Q. Bui. A multi-material proportional topology optimization approach for compliant mechanism problems. European Journal of Mechanics - A/Solids, 100, (2023). DOI: https://doi.org/10.1016/j.euromechsol.2023.104957
W. Zuo and K. Saitou. Multi-material topology optimization using ordered SIMP interpolation. Structural and Multidisciplinary Optimization, 55, (2), (2016), pp. 477–491. DOI: https://doi.org/10.1007/s00158-016-1513-3
S. Xu, J. Liu, B. Zou, Q. Li, and Y. Ma. Stress constrained multi-material topology optimization with the ordered SIMP method. Computer Methods in Applied Mechanics and Engineering, 373, (2021). DOI: https://doi.org/10.1016/j.cma.2020.113453
X. Gu, S. He, Y. Dong, and T. Song. An improved ordered SIMP approach for multi-scale concurrent topology optimization with multiple microstructures. Composite Structures, 287, (2022). DOI: https://doi.org/10.1016/j.compstruct.2022.115363
O. A. A. Silveira and L. F. Palma. Some considerations on multi-material topology optimization using ordered SIMP. Structural and Multidisciplinary Optimization, 65, (9), (2022). DOI: https://doi.org/10.1007/s00158-022-03379-7
C.-Y. Wu and K.-Y. Tseng. Topology optimization of structures using modified binary differential evolution. Structural and Multidisciplinary Optimization, 42, (6), (2010), pp. 939–953. DOI: https://doi.org/10.1007/s00158-010-0523-9
J. F. A. Madeira, H. Rodrigues, and H. Pina. Multi-objective optimization of structures topology by genetic algorithms. Advances in Engineering Software, 36, (1), (2005), pp. 21–28. DOI: https://doi.org/10.1016/j.advengsoft.2003.07.001
G.-C. Luh, C.-Y. Lin, and Y.-S. Lin. A binary particle swarm optimization for continuum structural topology optimization. Applied Soft Computing, 11, (2), (2011), pp. 2833–2844. DOI: https://doi.org/10.1016/j.asoc.2010.11.013
O. Sigmund. On the usefulness of non-gradient approaches in topology optimization. Structural and Multidisciplinary Optimization, 43, (5), (2011), pp. 589–596. DOI: https://doi.org/10.1007/s00158-011-0638-7
D. Guirguis and M. F. Aly. A derivative-free level-set method for topology optimization. Finite Elements in Analysis and Design, 120, (2016), pp. 41–56. DOI: https://doi.org/10.1016/j.finel.2016.06.002
D. Guirguis, W. W. Melek, and M. F. Aly. High-resolution non-gradient topology optimization. Journal of Computational Physics, 372, (2018), pp. 107–125. DOI: https://doi.org/10.1016/j.jcp.2018.06.025
P. Liu, Y. Yan, X. Zhang, Y. Luo, and Z. Kang. Topological design of microstructures using periodic material-field series-expansion and gradient-free optimization algorithm. Materials & Design, 199, (2021). DOI: https://doi.org/10.1016/j.matdes.2020.109437
B. Bochenek and K. Tajs-Zielinska. GOTICA - generation of optimal topologies by irregular cellular automata. Structural and Multidisciplinary Optimization, 55, (6), (2017). DOI: https://doi.org/10.1007/s00158-016-1614-z
D. C. Da, J. H. Chen, X. Y. Cui, and G. Y. Li. Design of materials using hybrid cellular automata. Structural and Multidisciplinary Optimization, 56, (1), (2017), pp. 131–137. DOI: https://doi.org/10.1007/s00158-017-1652-1
J. Jia, D. Da, C.-L. Loh, H. Zhao, S. Yin, and J. Xu. Multi-scale topology optimization for non-uniform microstructures with hybrid cellular automata. Structural and Multidisciplinary Optimization, 62, (2), (2020), pp. 757–770. DOI: https://doi.org/10.1007/s00158-020-02533-3
E. Biyikli and A. C. To. Proportional Topology Optimization: A new non-sensitivity method for solving stress constrained and minimum compliance problems and its implementation in MATLAB. PLOS ONE, 10, (12), (2015). DOI: https://doi.org/10.1371/journal.pone.0145041
H. Wang, W. Cheng, R. Du, S. Wang, and Y. Wang. Improved proportional topology optimization algorithm for solving minimum compliance problem. Structural and Multidisciplinary Optimization, 62, (2020), pp. 475–493. DOI: https://doi.org/10.1007/s00158-020-02504-8
W. Cheng, H. Wang, M. Zhang, and R. Du. Improved proportional topology optimization algorithm for minimum volume problem with stress constraints. Engineering Computations, 38, (1), (2020), pp. 392–412. DOI: https://doi.org/10.1108/EC-12-2019-0560
Z. Ullah, B. Ullah,W. Khan, and S. Islam. Proportional topology optimization with maximum entropy-based meshless method for minimum compliance and stress constrained problems. Engineering with Computers, 38, (6), (2022), pp. 5541–5561. DOI: https://doi.org/10.1007/s00366-022-01683-w
M. Cui, Y. Zhang, X. Yang, and C. Luo. Multi-material proportional topology optimization based on the modified interpolation scheme. Engineering with Computers, 34, (2017), pp. 287–305. DOI: https://doi.org/10.1007/s00366-017-0540-z
C. Talischi, G. H. Paulino, A. Pereira, and I. F. M. Menezes. Polygonal finite elements for topology optimization: A unifying paradigm. International Journal for Numerical Methods in Engineering, 82, (6), (2009), pp. 671–698. DOI: https://doi.org/10.1002/nme.2763
L. B. Veiga, F. Brezzi, A. Cangiani, G. Manizini, L. D. Marini, and A. Russo. Basis principles of virtual element methods. Mathematical Models and Methods in Applied Sciences, 23, (1), (2012), pp. 199–214. DOI: https://doi.org/10.1142/S0218202512500492
L. B. Veiga, F. Brezzi, and L. D. Marini. Virtual elements for linear elasticity problems. SIAM Journal on Numerical Analysis, 51, (2013), pp. 794–812. DOI: https://doi.org/10.1137/120874746
H. Chi, A. Pereira, I. F. M. Menezes, and G. H. Paulino. Virtual element method (VEM)-based topology optimization: an integrated framework. Structural and Multidisciplinary Optimization, 62, (3), (2019), pp. 1089–1114. DOI: https://doi.org/10.1007/s00158-019-02268-w
A. L. Gain, C. Talischi, and G. H. Paulino. On the Virtual Element Method for three-dimensional linear elasticity problems on arbitrary polyhedral meshes. Computer Methods in Applied Mechanics and Engineering, 282, (2014), pp. 132–160. DOI: https://doi.org/10.1016/j.cma.2014.05.005
A. Ortiz-Bernardin, C. Alvarez, N. Hitschfeld-Kahler, A. Russo, R. Silva-Valenzuela, and E. Olate-Sanzana. Veamy: an extensible object-oriented C++ library for the virtual element method. Numerical Algorithms, 82, (2019), pp. 1189–1220. DOI: https://doi.org/10.1007/s11075-018-00651-0
H. Chi, L. B. Veiga, and G. H. Paulino. Some basic formulations of the virtual element method (VEM) for finite deformations. Computer Methods in Applied Mechanics and Engineering, 318, (2017), pp. 148–192. DOI: https://doi.org/10.1016/j.cma.2016.12.020
E. Artioli, L. B. Veiga, C. Lovadina, and E. Sacco. Arbitrary order 2D virtual elements for polygonal meshes: Part II, inelastic problem. Computational Mechanics, 60, (4), (2017), pp. 643–657. DOI: https://doi.org/10.1007/s00466-017-1429-9
P. Wriggers, W. T. Rust, and B. D. Reddy. A virtual element method for contact. Computational Mechanics, 58, (6), (2016), pp. 1039–1050. DOI: https://doi.org/10.1007/s00466-016-1331-x
M. F. Benedetto, A. Caggiano, and G. Etse. Virtual elements and zero thickness interfacebased approach for fracture analysis of heterogeneous materials. Computer Methods in Applied Mechanics and Engineering, 338, (2018), pp. 41–67. DOI: https://doi.org/10.1016/j.cma.2018.04.001
P. F. Antonieti, M. Bruggi, S. Scacchi, and M. Verani. On the virtual element method for topology optimization on polygonal meshes: A numerical study. Computers & Mathematics with Applications, 74, (5), (2017), pp. 1091–1109. DOI: https://doi.org/10.1016/j.camwa.2017.05.025
T. M. Tuan, M. N. Nguyen, T. Q. Bui, and H. Q. Nguyen. An enhanced proportional topology optimization with virtual elements: Formulation and numerical implementation. Finite Elements in Analysis and Design, 222, (2023). DOI: https://doi.org/10.1016/j.finel.2023.103958
C. Talischi, G. H. Paulino, A. Pereira, and I. F. M. Menezes. PolyMesher: A general-purpose mesh generator for polygonal elements written in Matlab. Structural and Multidisciplinary Optimization, 45, (3), (2012), pp. 309–328. DOI: https://doi.org/10.1007/s00158-011-0706-z
O. Sigmund. On benchmarking and good scientific practise in topology optimization. Structural and Multidisciplinary Optimization, 65, (2022). DOI: https://doi.org/10.1007/s00158-022-03427-2
T. T. Banh and D. Lee. Topology optimization of multi-directional variable thickness thin plate with multiple materials. Structural and Multidisciplinary Optimization, 59, (5), (2019), pp. 1503–1520. DOI: https://doi.org/10.1007/s00158-018-2143-8
Downloads
Published
How to Cite
Issue
Section
Categories
License
This work is licensed under a Creative Commons Attribution-ShareAlike 4.0 International License.
