A staggered local damage model for fracture analysis in bi-material structures
Author affiliations
DOI:
https://doi.org/10.15625/0866-7136/21007Keywords:
enhanced local damage, bi-material structures, fracture analysis, staggered schemeAbstract
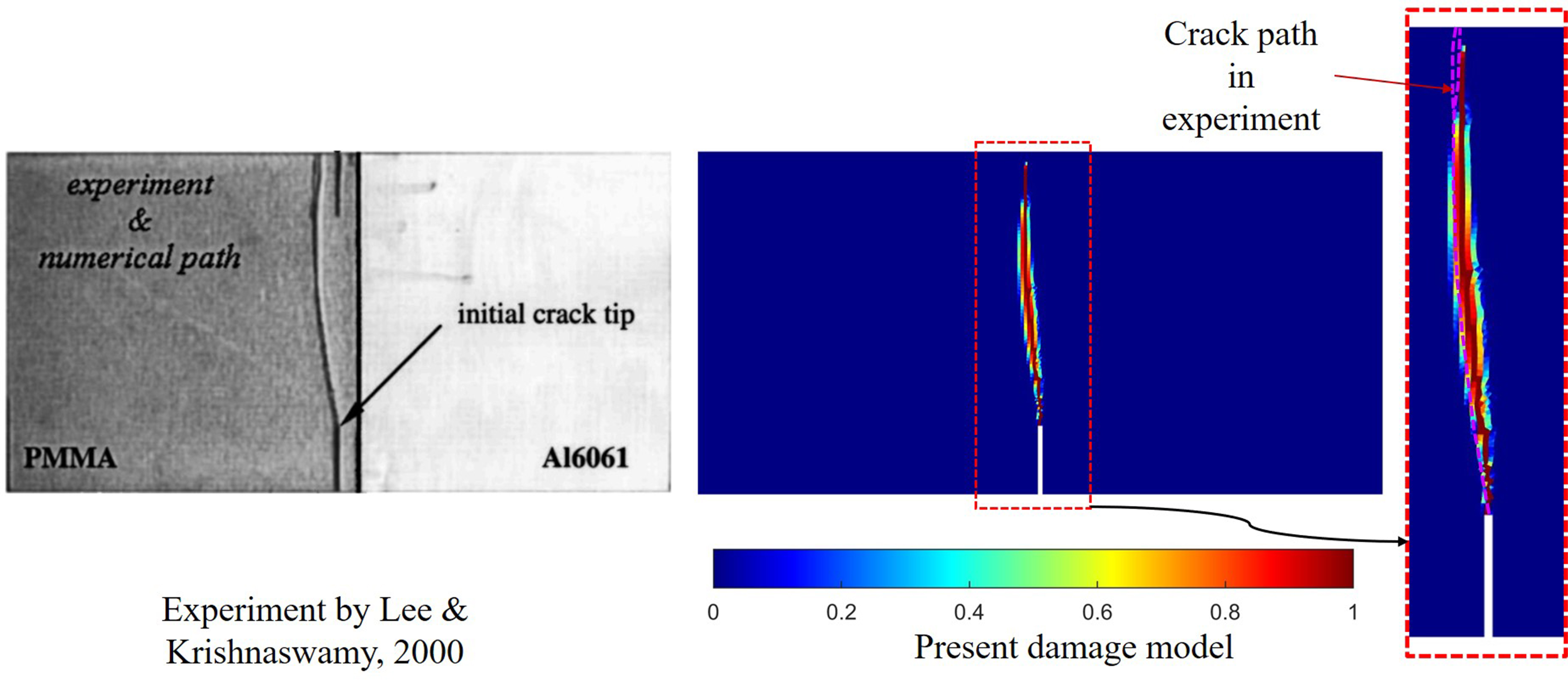
This article is devoted to extension of the recently developed enhanced local damage model for failure prediction in bi-material structures. Compared to non-local models, the enhanced local model offers lower computational cost while the inherent mesh-dependency issue is treated. By defining equivalent strain based on the bi-energy norm concept and Mazars’s criterion, which considers both tensile and compressive strain components, the model aligns with the behavior of quasi-brittle materials. The state of material point is indicated by a damage parameter, ranging from 0 to 1, to represent the evolution from being fully intact to complete failure. An efficient staggered scheme is introduced, in which the equilibrium equation and the update of damage parameter are decoupled. The proposed model is validated with a series of three-point bending experimental tests on PMMA/Al6061 specimens reported by Lee and Krishnaswamy (2000). Good agreement is observed between the proposed model and experimental data, as well as numerical results from other authors, in crack path prediction.
Downloads
References
[1] L. M. Kachanov and D. Krajcinovic. Introduction to continuum damage mechanics. Journal of Applied Mechanics, 54, (1987), pp. 481–481. https://doi.org/10.1115/1.3173053.
[2] J. Lemaitre and R. Desmorat. Engineering damage mechanics: ductile, creep, fatigue and brittle failures. Springer Science & Business Media, (2006).
[3] M. Jirásek and B. Patzák. Consistent tangent stiffness for nonlocal damage models. Computers & Structures, 80, (2002), pp. 1279–1293. https://doi.org/10.1016/s0045-7949(02)00078-0.
[4] C. Giry, F. Dufour, and J. Mazars. Stress-based nonlocal damage model. International Journal of Solids and Structures, 48, (2011), pp. 3431–3443. https://doi.org/10.1016/j.ijsolstr.2011.08.012.
[5] M. Kurumatani, K. Terada, J. Kato, T. Kyoya, and K. Kashiyama. An isotropic damage model based on fracture mechanics for concrete. Engineering Fracture Mechanics, 155, (2016), pp. 49– 66. https://doi.org/10.1016/j.engfracmech.2016.01.020.
[6] M. V. Pham, M. N. Nguyen, and T. Q. Bui. Numerical simulation of localized quasi-brittle fracture with an enhanced bi-energy norm based equivalent strain. Engineering Fracture Mechanics, 288, (2023), 109340. https://doi.org/10.1016/j.engfracmech.2023.109340.
[7] M. V. Pham, M. N. Nguyen, and T. Q. Bui. A novel thermo-mechanical local damage model for quasi-brittle fracture analysis. Theoretical and Applied Fracture Mechanics, 130, (2024), 104329. https://doi.org/10.1016/j.tafmec.2024.104329.
[8] H. Lee and S. Krishnaswamy. Quasi-static propagation of subinterfacial cracks. Journal of Applied Mechanics, 67, (2000), pp. 444–452. https://doi.org/10.1115/1.1311275.
[9] M. Kikuchi, Y. Wada, and Y. Li. Crack growth simulation in heterogeneous material by S-FEM and comparison with experiments. Engineering Fracture Mechanics, 167, (2016), pp. 239–247. https://doi.org/10.1016/j.engfracmech.2016.03.038.
[10] A. Rajput, A. Subhash Shedbale, and D. Khan. A robust staggered localizing gradient enhanced isotropic damage model for failure prediction in heterogeneous materials. Engineering Fracture Mechanics, 293, (2023), 109708. https://doi.org/10.1016/j.engfracmech.2023.109708.
[11] J. H. P. de Vree, W. A. M. Brekelmans, and M. A. J. van Gils. Comparison of nonlocal approaches in continuum damage mechanics. Computers & Structures, 55, (1995), pp. 581–588. https://doi.org/10.1016/0045-7949(94)00501-s.
[12] J. Mazars, F. Hamon, and S. Grange. A new 3D damage model for concrete under mono-tonic, cyclic and dynamic loadings. Materials and Structures, 48, (2014), pp. 3779–3793. https://doi.org/10.1617/s11527-014-0439-8.
[13] T. H. A. Nguyen, T. Q. Bui, and S. Hirose. Smoothing gradient damage model with evolving anisotropic nonlocal interactions tailored to low-order finite elements. Computer Methods in Applied Mechanics and Engineering, 328, (2018), pp. 498–541. https://doi.org/10.1016/j.cma.2017.09.019.
[14] Y. Wang and H. Waisman. From diffuse damage to sharp cohesive cracks: A coupled XFEM framework for failure analysis of quasi-brittle materials. Computer Methods in Applied Mechanics and Engineering, 299, (2016), pp. 57–89. https://doi.org/10.1016/j.cma.2015.10.019.
[15] T. Q. Bui and H. T. Tran. Dynamic brittle fracture with a new energy limiter-based scalar damage model. Computational Mechanics, 69, (2022), pp. 1323–1346. https://doi.org/10.1007/s00466-022-02143-4.
Downloads
Published
How to Cite
License

This work is licensed under a Creative Commons Attribution-ShareAlike 4.0 International License.









