Higher-order stochastic averaging for investigating a vehicle suspension system with nonlinear damping and stiffness
Author affiliations
DOI:
https://doi.org/10.15625/0866-7136/21137Keywords:
higher-order stochastic averaging (HOSA), quarter car model, nonlinear suspension, random excitationAbstract
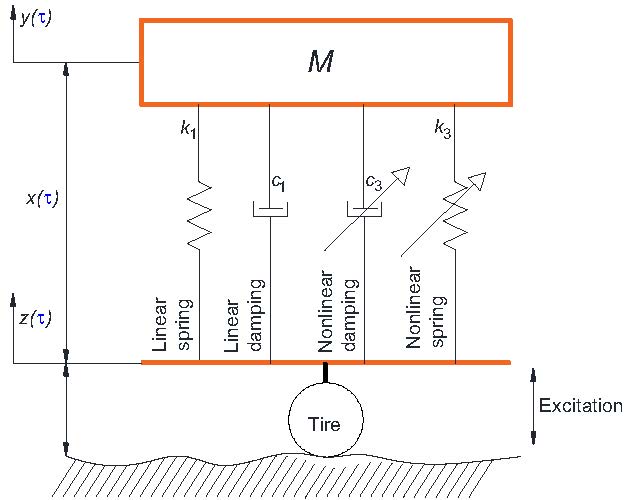
The paper deals with a quarter-car model with nonlinear damping and stiffness under white noise base excitation using the higher-order stochastic averaging method for analyzing approximate responses. Recently, a novel higher-order averaging procedure has been developed to find analytically the first-, second-, and third-order stationary joint probability density functions (PDF) of amplitude and full phase by solving the corresponding Fokker-Planck-Kolmogorov (FPK) equation, and it will be extended to the nonlinear quarter-car model. Accordingly, the mean-square responses such as the displacement, and velocity of the sprung mass can be obtained analytically. The influences of excitation intensity on the dynamic responses, as well as the variations of linear and nonlinear damping, are analyzed. A very satisfactory agreement is found between the accuracy of the solutions corresponding to higher-order stochastic averaging and that of Monte Carlo simulation.
Downloads
References
[1] A. Khazaie, N. Hussaini, H. Marzbani, and R. N. Jazar. Quarter car suspension model with provision for loss of contact with the road. In Nonlinear Approaches in Engineering Applications, Springer International Publishing, (2018), pp. 167–208. https://doi.org/10.1007/978-3-319- 69480-1 7.
[2] S. Yang, L. Chen, and S. Li. Dynamics of vehicle-road coupled system. Springer Berlin Heidelberg, (2015). https://doi.org/10.1007/978-3-662-45957-7.
[3] J. C. Dixon. The shock absorber handbook. Wiley, (2007). https://doi.org/10.1002/9780470516430.
[4] N. Panananda, N. S. Ferguson, and T. P. Waters. The effect of cubic damping in an automotive vehicle suspension model. In International Symposium on the Computational Modelling and Analysis of Vehicle Body Noise and Vibration, Brighton, United Kingdom, (2012).
[5] Z. Lozia and P. Zdanowicz. Optimization of damping in the passive automotive suspension system with using two quarter-car models. IOP Conference Series: Materials Science and Engineering, 148, (2016), p. 012014. https://doi.org/10.1088/1757-899x/148/1/012014.
[6] M. Silveira, P. Wahi, and J. C. M. Fernandes. Effects of asymmetrical damping on a 2 dof quarter-car model under harmonic excitation. Communications in Nonlinear Science and Numerical Simulation, 43, (2017), pp. 14–24. https://doi.org/10.1016/j.cnsns.2016.06.029.
[7] S. Li, S. Yang, and W. Guo. Investigation on chaotic motion in hysteretic non-linear suspension system with multi-frequency excitations. Mechanics Research Communications, 31, (2004), pp. 229–236. https://doi.org/10.1016/j.mechrescom.2003.10.002.
[8] U. v. Wagner. On non-linear stochastic dynamics of quarter car models. International Journal of Non-Linear Mechanics, 39, (2004), pp. 753–765. https://doi.org/10.1016/s0020-7462(03)00039-8.
[9] M. Silveira, J. M. Balthazar, and J. C. Moraes Fernandes. Stochastic analysis of 1-DOF vehicle suspension system employing asymmetrical damping. In Proceedings of the 24th ABCM International Congress of Mechanical Engineering, ABCM, COB17, (2017). https://doi.org/10.26678/abcm.cobem2017.cob17-0150.
[10] Y. A. Mitropolskii, N. V. Dao, and N. D. Anh. Nonlinear oscillations in systems of arbitrary order. Naukova-Dumka, Kiev, (1992). (in Russian).
[11] N. D. Anh. Higher order averaging method of coefficients in Fokker-Planck equation. Sadhana, 20, (1995), pp. 373–387. https://doi.org/10.1007/bf02823197.
[12] N. D. Anh, N. N. Linh, N. N. Hieu, N. Van Manh, and A. T. Nguyen. Application of high order averaging method to Van der Pol oscillator. In Advances in Asian Mechanism and Machine Science, Springer International Publishing, (2021), pp. 825–834. https://doi.org/10.1007/978- 3-030-91892-7 79.
[13] N. V. Manh, N. N. Linh, A. T. Nguyen, and N. D. Anh. Higher-order averaging procedure for performance analysis of a mono-stable Duffing piezoelectric energy harvesting system under white noise excitation. Mechanics Research Communications, 131, (2023), p. 104157. https://doi.org/10.1016/j.mechrescom.2023.104157.
[14] C. J. Dodds and J. D. Robson. The description of road surface roughness. Journal of Sound and Vibration, 31, (2), (1973), pp. 175–183. https://doi.org/10.1016/s0022-460x(73)80373-6.
Downloads
Published
How to Cite
License

This work is licensed under a Creative Commons Attribution-ShareAlike 4.0 International License.




