A novel criterion for crack detection in beam structures by frequency response functions
Author affiliations
DOI:
https://doi.org/10.15625/0866-7136/19040Keywords:
crack identification, frequency response function, frequency domain assurance criterion, contour methodAbstract
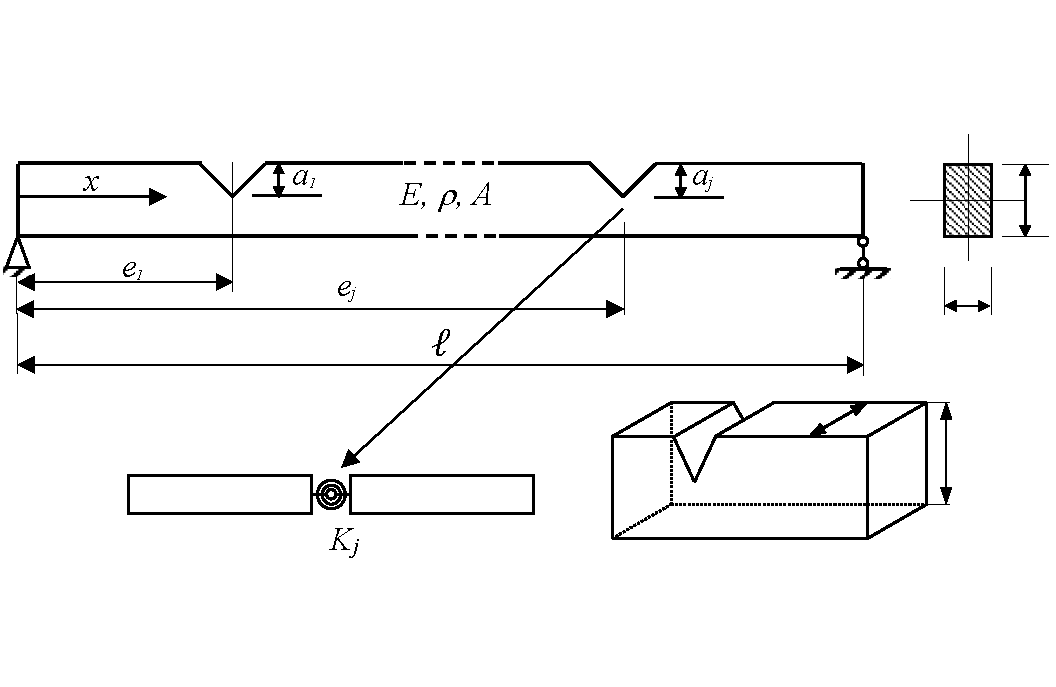
The frequency response function (FRF) is a fruitful attribute that includes almost all dynamical characteristics of a structure such as natural frequencies and modes, damping coefficients, or resonance and antiresonance conceptions. However, the complex feature of FRF has not been thoroughly employed for structural damage detection. In the present study, a novel indicator extracted from FRFs of beam structures is developed for crack identification. The damage indicator originated from the well-known mode assurance criterion (MAC) and therefore it is termed spectral assurance criterion (SAC). First, a coherence coefficient calculated from FRFs of intact and damaged beams and called herein spectral damage index (SDI) is analyzed for examining sensitivity of FRFs to crack. Then, SAC calculated for different FRFs of the same damaged structure is employed for crack detection by the so-called contour method. Results obtained in numerical examples of the crack detection problem show that SAC is really a novel and efficient criterion for crack identification in beams from measured FRFs.
Downloads
Metrics
References
Z. Wang, R. M. Lin, and M. K. Lim. Structural damage detection using measured FRF data. Computer Methods in Applied Mechanics and Engineering, 147, (1997), pp. 187–197. DOI: https://doi.org/10.1016/S0045-7825(97)00013-3
S. K. Thyagarajan, M. J. Schulz, P. F. Pai, and J. Chung. Detecting structural damage using frequency response functions. Journal of Sound and Vibration, 210, (1998), pp. 162–170. DOI: https://doi.org/10.1006/jsvi.1997.1308
R. P. C. Sampaio, N. M. M. Maia, and J. M. M. Silva. Damage detection using the frequencyresponse-function curvature method. Journal of Sound and Vibration, 226, (1999), pp. 1029–1042. DOI: https://doi.org/10.1006/jsvi.1999.2340
U. Lee and J. Shin. A frequency response function-based structural damage identification method. Computers & Structures, 80, (2002), pp. 117–132. DOI: https://doi.org/10.1016/S0045-7949(01)00170-5
N.-G. Park and Y.-S. Park. Detection using spatially incomplete frequency response functions. Mechanical Systems and Signal Processing, 17, (2003), pp. 519–532. DOI: https://doi.org/10.1006/mssp.2001.1423
H. Y. Hwang and C. Kim. Damage detection in structures using a few frequency response measurements. Journal of Sound and Vibration, 270, (2004), pp. 1–14. DOI: https://doi.org/10.1016/S0022-460X(03)00190-1
X. Liu, N. A. J. Lieven, and P. J. Escamilla-Ambrosio. Frequency response function shapebased methods for structural damage localisation. Mechanical Systems and Signal Processing, 23, (2009), pp. 1243–1259. DOI: https://doi.org/10.1016/j.ymssp.2008.10.002
R. P. Bandara, T. H. T. Chan, and D. P. Thambiratnam. Structural damage detection method using frequency response functions. Structural Health Monitoring, 13, (2014), pp. 418–429. DOI: https://doi.org/10.1177/1475921714522847
M. Dilena, M. P. Limongelli, and A. Morassi. Damage localization in bridges via the FRF interpolation method. Mechanical Systems and Signal Processing, 52-53, (2015), pp. 162–180. DOI: https://doi.org/10.1016/j.ymssp.2014.08.014
N. T. Khiem, P. T. Hang, and L. K. Toan. Crack detection in pile by measurements of frequency response function. Nondestructive Testing and Evaluation, 31, (2015), pp. 122–141. DOI: https://doi.org/10.1080/10589759.2015.1081904
R. Pascual, J.-C. Golinval, and M. Razeto. A frequency domain correlation technique for model correlation and updating. In 15th International Modal Analysis Conference (IMAC XV), (1997), pp. 587–592.
D. Fotsch and D. J. Ewins. Application of MAC in the frequency domain. CiteSeerX, The College of Information Sciences and Technology, The Pennsylvania State University, (2000).
R. J. Allemang. The modal assurance criterion–twenty years of use and abuse. Sound and vibration, 37, (8), (2003), pp. 14–23.
S. Lei, K. Mao, L. Li, W. Xiao, and B. Li. Direct method for second-order sensitivity analysis of modal assurance criterion. Mechanical Systems and Signal Processing, 76-77, (2016), pp. 441–454. DOI: https://doi.org/10.1016/j.ymssp.2016.02.003
A. Messina, E. J. Williams, and T. Contursi. Structural damage detection by a sensitivity and statistical-based method. Journal of Sound and Vibration, 216, (1998), pp. 791–808. DOI: https://doi.org/10.1006/jsvi.1998.1728
E. J. Williams and A. Messina. Applications of the multiple damage location assurance criterion. Key Engineering Materials, 167-168, (1999), pp. 256–264. DOI: https://doi.org/10.4028/www.scientific.net/KEM.167-168.256
R. P. C. Sampaio, N. M. M. Maia, and J. M. M. Silva. The frequency domain assurance criterion as a tool for damage detection. Key Engineering Materials, 245-246, (2003), pp. 69–76. DOI: https://doi.org/10.4028/www.scientific.net/KEM.245-246.69
I. Duvnjak, D. Damjanovic, M. Bartolac, and A. Skender. Mode shape-based damage detection method (MSDI): experimental validation. Applied Sciences, 11, (2021). DOI: https://doi.org/10.3390/app11104589
N. T. Khiem. Vibrations of cracked functionally graded beams: General solution and application – A review. Vietnam Journal of Mechanics, 44, (2022), pp. 317–347. DOI: https://doi.org/10.15625/0866-7136/17986
V. B. Zaalishvili and I. D. Muzaeb. One effective method for solving initialboundary problems of transverse vibrations of a beam, taking into account its internal resistance. Geology and Geophysics of Russian South, 13, (2023), pp. 55–66. DOI: https://doi.org/10.46698/VNC.2023.63.12.005
Downloads
Published
How to Cite
License
This work is licensed under a Creative Commons Attribution-ShareAlike 4.0 International License.
