Gravity-driven wet granular free-surface flows down an inclined plane: Effects of the inclination angle
Author affiliations
DOI:
https://doi.org/10.15625/0866-7136/16696Keywords:
capillary bridge, discrete element method, force distribution, fluid-like, granular flow, solid-likeAbstract
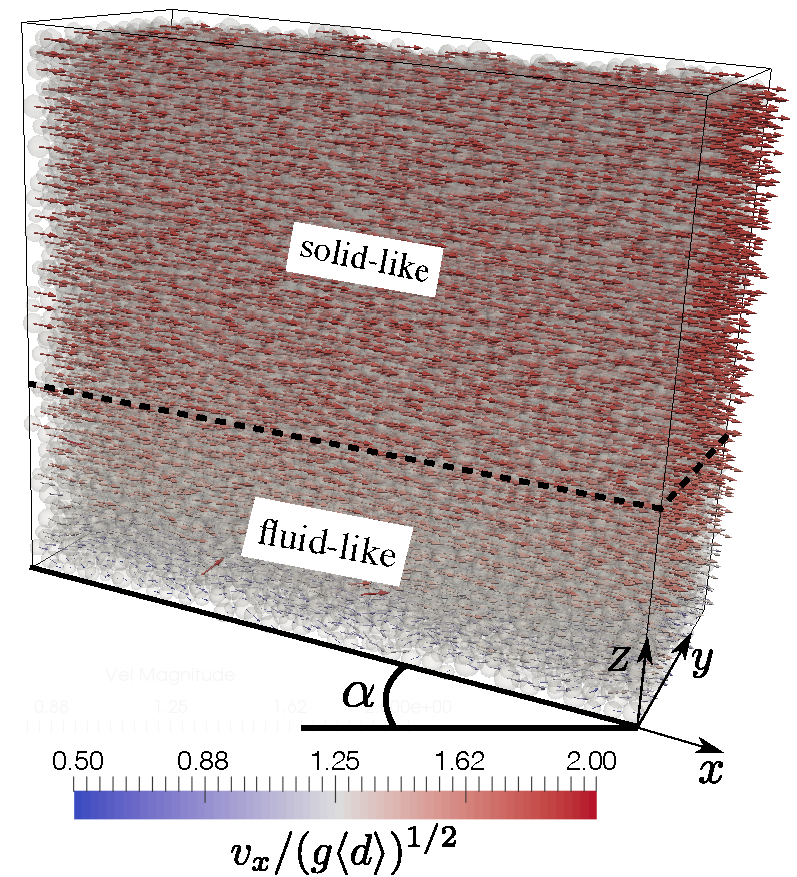
Wet granular materials flowing down an inclined plane are omnipresent in multi-field engineering. Although extensive research has been carried out to investigate the flowability of such flows, our understanding of the flows like landslides is limited due to the presence of the cohesive forces between particles and the arbitrarity of inclination angle. In this paper, we explore the effects of the inclination angle on the velocity profiles and force distribution of the gravity-driven wet granular free-surface flows in the steady-flowing state by means of an extensive discrete element method with the inclusion of the capillary cohesion law. This capillary cohesion law is enhanced by the capillary attraction force due to the presence of the liquid bridges between near-neighboring particles. The results show that the mobility of wet granular materials is strongly controlled by the inclination angle due to the domination of the gravity effects of particles as compared to the cohesion effects and rough effects of the inclined surface. These observations are consistent with the previous experimental work done on the granular collapse on an inclined plane. Furthermore, in its steady-state flow, the granular materials separate stably into two different flowing regions: solid-like and fluid-like flows, and the depth of these flows strongly depends on the values of the inclination angle. More interestingly, the inclination angle also strongly governs the density and intensity of the tensile and compressive components of the normal forces and tangential forces in both solid-like and fluid-like regions with different characteristics.
Downloads
Metrics
References
O. Pouliquen. Scaling laws in granular flows down rough inclined planes. Physics of Fluids, 11, (3), (1999), pp. 542–548.
DOI: https://doi.org/10.1063/1.869928
O. Pouliquen. Velocity correlations in dense granular flows. Physical Review Letters, 93, (2004).
DOI: https://doi.org/10.1103/PhysRevLett.93.248001
C. Zhu, Y. Huang, and J. Sun. Solid-like and liquid-like granular flows on inclined surfaces under vibration–Implications for earthquake-induced landslides. Computers and Geotechnics, 123, (2020).
DOI: https://doi.org/10.1016/j.compgeo.2020.103598
D. Ertas. and T. C. Halsey. Granular gravitational collapse and chute flow. Europhysics Letters (EPL), 60, (2002), pp. 931–937.
DOI: https://doi.org/10.1209/epl/i2002-00307-8
C. Goujon, N. Thomas, and B. Dalloz-Dubrujeaud. Monodisperse dry granular flows on inclined planes: Role of roughness. The European Physical Journal E, 11, (2003), pp. 147–157.
DOI: https://doi.org/10.1140/epje/i2003-10012-0
M. Y. Louge. Model for dense granular flows down bumpy inclines. Physical Review E, 67, (2003).
DOI: https://doi.org/10.1103/PhysRevE.67.061303
C. Cassar, M. Nicolas, and O. Pouliquen. Submarine granular flows down inclined planes. Physics of Fluids, 17, (10), (2005).
DOI: https://doi.org/10.1063/1.2069864
T. Börzsönyi and R. E. Ecke. Flow rule of dense granular flows down a rough incline. Physical Review E, 76, (3), (2007).
DOI: https://doi.org/10.1103/PhysRevE.76.031301
R. Delannay, M. Louge, P. Richard, N. Taberlet, and A. Valance. Towards a theoretical picture of dense granular flows down inclines. Nature Materials, 6, (2007), pp. 99–108.
DOI: https://doi.org/10.1038/nmat1813
GDR-MiDi. On dense granular flows. The European Physical Journal E, 14, (2004), pp. 341–365.
DOI: https://doi.org/10.1140/epje/i2003-10153-0
O. Pouliquen, C. Cassar, P. Jop, Y. Forterre, and M. Nicolas. Flow of dense granular material: towards simple constitutive laws. Journal of Statistical Mechanics: Theory and Experiment, 2006, (07), (2006).
DOI: https://doi.org/10.1088/1742-5468/2006/07/P07020
P. Jop, Y. Forterre, and O. Pouliquen. A constitutive law for dense granular flows. Nature, 441, (2006), pp. 727–730.
DOI: https://doi.org/10.1038/nature04801
L. E. Silbert, D. Ertas., G. S. Grest, T. C. Halsey, D. Levine, and S. J. Plimpton. Granular flow down an inclined plane: Bagnold scaling and rheology. Physical Review E, 64, (5), (2001).
DOI: https://doi.org/10.1103/PhysRevE.64.051302
Y. Zhang and C. S. Campbell. The interface between fluid-like and solid-like behaviour in two-dimensional granular flows. Journal of Fluid Mechanics, 237, (1992), pp. 541–568.
DOI: https://doi.org/10.1017/S0022112092003525
P. G. Rognon, J.-N. Roux, M. Naaim, and F. Chevoir. Dense flows of cohesive granular materials. Journal of Fluid Mechanics, 596, (2008), pp. 21–47.
DOI: https://doi.org/10.1017/S0022112007009329
S. Mandal, M. Nicolas, and O. Pouliquen. Insights into the rheology of cohesive granular media. Proceedings of the National Academy of Sciences, 117, (2020), pp. 8366–8373.
DOI: https://doi.org/10.1073/pnas.1921778117
H. Moharamkhani, R. Sepehrinia, M. Taheri, M. Jalalvand, M. Brinkmann, and S. M. Vaez Allaei. Ordered/disordered monodisperse dense granular flow down an inclined plane: dry versus wet media in the capillary bridge regime. Granular Matter, 23, (3), (2021), pp. 1–16.
DOI: https://doi.org/10.1007/s10035-021-01115-4
R. Brewster, G. S. Grest, J. W. Landry, and A. J. Levine. Plug flow and the breakdown of Bagnold scaling in cohesive granular flows. Physical Review E, 72, (6), (2005).
DOI: https://doi.org/10.1103/PhysRevE.72.061301
L. E. Silbert, J. W. Landry, and G. S. Grest. Granular flow down a rough inclined plane: Transition between thin and thick piles. Physics of Fluids, 15, (2003), pp. 1–10.
DOI: https://doi.org/10.1063/1.1521719
S. H. Chou and S. S. Hsiau. Experimental analysis of the dynamic properties of wet granular matter in a rotating drum. Powder Technology, 214, (2011), pp. 491–499.
DOI: https://doi.org/10.1016/j.powtec.2011.09.010
P. A. Cundall and O. D. L. Strack. A discrete numerical model for granular assemblies. Géotechnique, 29, (1979), pp. 47–65.
DOI: https://doi.org/10.1680/geot.1979.29.1.47
F. Radjai and F. Dubois. Discrete-element modeling of granular materials. Wiley-Iste, (2011).
T.-T. Vo. Rheology and granular texture of viscoinertial simple shear flows. Journal of Rheology, 64, (5), (2020), pp. 1133–1145.
DOI: https://doi.org/10.1122/8.0000033
S. Luding. Collisions & contacts between two particles. In Physics of dry granular media, pp. 285–304. Springer, (1998).
DOI: https://doi.org/10.1007/978-94-017-2653-5_20
H. J. Herrmann and S. Luding. Modeling granular media on the computer. Continuum Mechanics and Thermodynamics, 10, (1998), pp. 189–231.
DOI: https://doi.org/10.1007/s001610050089
T.-T. Vo, T. L. Vu, and P. Mutabaruka. Effects of size polydispersity on segregation of spherical particles in rotating drum. The European Physical Journal E, 44, (6), (2021), pp. 1–10.
DOI: https://doi.org/10.1140/epje/s10189-021-00091-0
V. Richefeu, M. S. E. Youssoufi, R. Peyroux, and F. Radjaï. A model of capillary cohesion for numerical simulations of 3D polydisperse granular media. International Journal for Numerical and Analytical Methods in Geomechanics, 32, (2008), pp. 1365–1383.
DOI: https://doi.org/10.1002/nag.674
T.-T. Vo. Erosion dynamics of wet particle agglomerates. Computational Particle Mechanics, 8, (3), (2021), pp. 601–612.
DOI: https://doi.org/10.1007/s40571-020-00357-y
J. Duran, A. Reisinger, and P. de Gennes. Sands, powders, and grains: an introduction to the physics of granular materials. Partially Ordered Systems, Springer New York, (1999).
DOI: https://doi.org/10.1007/978-1-4612-0499-2_1
T. T. Vo, S. Nezamabadi, P. Mutabaruka, J.-Y. Delenne, and F. Radjai. Additive rheology of complex granular flows. Nature Communications, 11, (1), (2020), pp. 1–8.
DOI: https://doi.org/10.1038/s41467-020-15263-3
J. ShÅNafer, S. Dippel, and D. E.Wolf. Force schemes in simulations of granular materials. Journal de Physique I, 6, (1996), pp. 5–20.
DOI: https://doi.org/10.1051/jp1:1996129
T. K. Nguyen, A. A. Claramunt, D. Caillerie, G. Combe, S. D. Pont, J. Desrues, and V. Richefeu. FEM × DEM: a new efficient multi-scale approach for geotechnical problems with strain localization. EPJ Web of Conferences, 140, (2017).
DOI: https://doi.org/10.1051/epjconf/201714011007
T.-T. Vo, C. T. Nguyen, T.-K. Nguyen, V. M. Nguyen, and T. L. Vu. Impact dynamics and power-law scaling behavior of wet agglomerates. Computational Particle Mechanics, 9, (3), (2022), pp. 537–550.
DOI: https://doi.org/10.1007/s40571-021-00427-9
C. M. Donahue, C. M. Hrenya, and R. H. Davis. Stokes’s cradle: Newton’s cradle with liquid coating. Physical review letters, 105, (3), (2010).
DOI: https://doi.org/10.1103/PhysRevLett.105.034501
C. M. Donahue, R. H. Davis, A. A. Kantak, and C. M. Hrenya. Mechanisms for agglomeration and deagglomeration following oblique collisions of wet particles. Physical Review E, 86, (2), (2012).
DOI: https://doi.org/10.1103/PhysRevE.86.021303
T. Mikami, H. Kamiya, and M. Horio. Numerical simulation of cohesive powder behavior in a fluidized bed. Chemical Engineering Science, 53, (1998), pp. 1927–1940.
DOI: https://doi.org/10.1016/S0009-2509(97)00325-4
G. Lian, C. Thornton, and M. J. Adams. A theoretical study of the liquid bridge forces between two rigid spherical bodies. Journal of Colloid and Interface Science, 161, (1993), pp. 138–147.
DOI: https://doi.org/10.1006/jcis.1993.1452
V. Richefeu, F. Radjaı, and M. S. El Youssoufi. Stress transmission in wet granular materials. The European Physical Journal E, 21, (4), (2006), pp. 359–369.
DOI: https://doi.org/10.1140/epje/i2006-10077-1
V. Richefeu, M. S. El Youssoufi, and F. Radjai. Shear strength properties of wet granular materials. Physical Review E, 73, (5), (2006).
DOI: https://doi.org/10.1103/PhysRevE.73.051304
J. Happel and H. Brenner. Low Reynolds number hydrodynamics. Martinus Nijhoff Publishers, The Hague, the Netherlands, (1983).
T.-T. Vo and C. T. Nguyen. Characteristics of force transmission in cohesive agglomerates impacting a rigid surface. Mechanics Research Communications, 117, (2021).
DOI: https://doi.org/10.1016/j.mechrescom.2021.103773
Downloads
Published
How to Cite
Issue
Section
License
This work is licensed under a Creative Commons Attribution-ShareAlike 4.0 International License.
