A numerical study of the solidification process of a retracting fluid filament
Author affiliations
DOI:
https://doi.org/10.15625/0866-7136/16393Keywords:
front-tracking method, fluid filament, cold flat surfaceAbstract
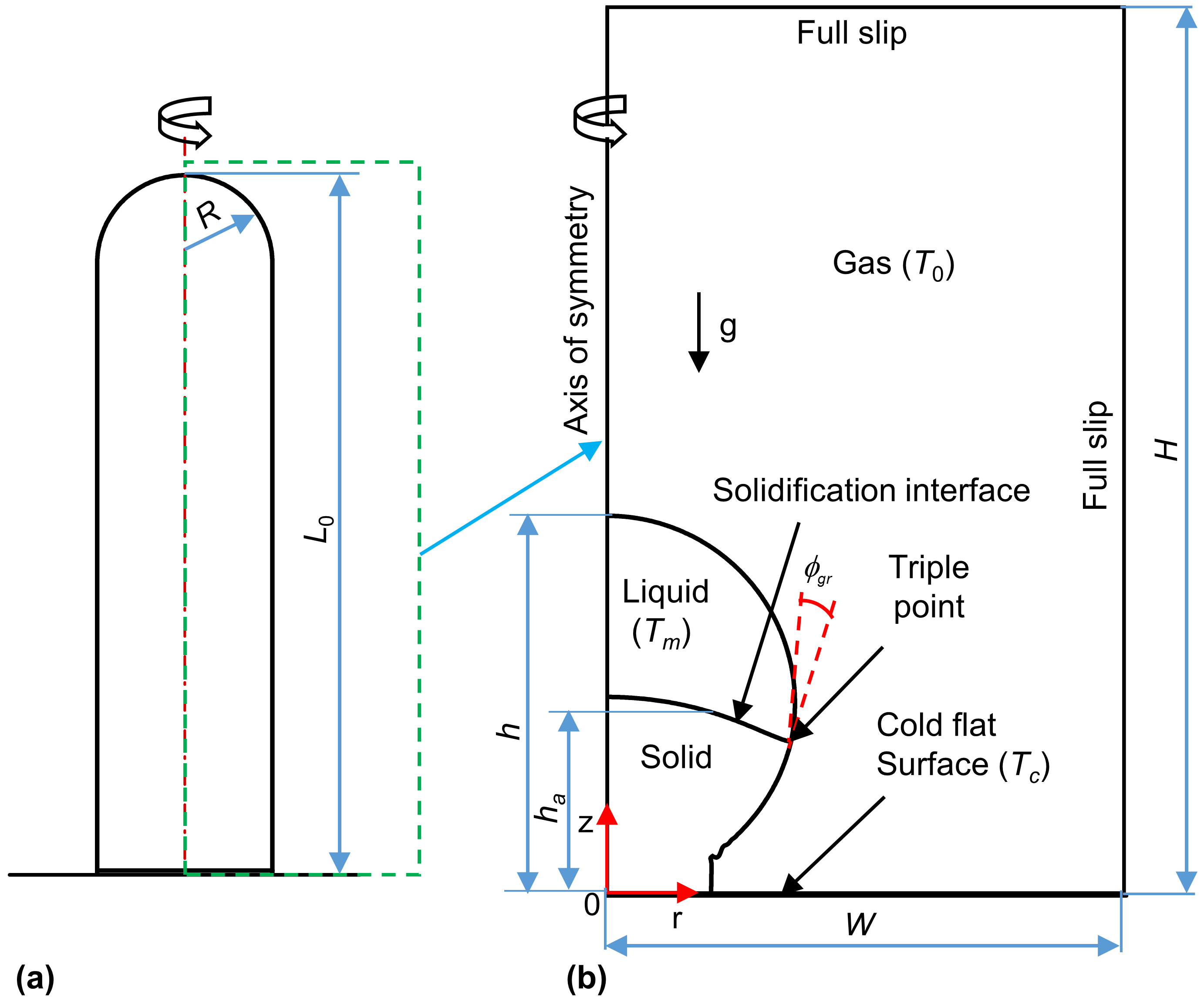
In this study, the retraction and solidification of a fluid filament are studied by a front-tracking method/finite difference scheme. The interface between two phases is handled by connected points (Lagrangian grid), which move on a fixed grid domain (Eulerian grid). The Navier-Stokes and energy equations are solved to simulate the problem. Initially, the fluid filament has a shape as half of a cylindrical capsule contact with a cold flat surface. We consider the effect of the aspect ratio (Ar) on the solidification of the fluid filament. It is found that an increase in the aspect ratio (Ar) in the range of 2 – 14 causes the retraction length to increase. The rate of the solidification of a fluid filament decreases when the Ar ratio increases. The solidification time, the solidification height and the tip angle of the fluid filament under the influence of the aspect ratio are also considered. After complete solidification, a small protrusion on the top of the solidified fluid filament is found.
Downloads
References
D. J. McClements. Advances in fabrication of emulsions with enhanced functionality using structural design principles. Current Opinion in Colloid & Interface Science, 17, (2012), pp. 235–245.
A. A. Maan, K. Schroën, and R. Boom. Spontaneous droplet formation techniques for monodisperse emulsions preparation – perspectives for food applications. Journal of Food Engineering, 107, (2011), pp. 334–346.
G. Muschiolik. Multiple emulsions for food use. Current Opinion in Colloid & Interface Science, 12, (2007), pp. 213–220.
W. J. Jasinski, S. C. Noe, M. S. Selig, and M. B. Bragg. Wind turbine performance under icing conditions. Journal of Solar Energy Engineering, 120, (1998), pp. 60–65.
Y. Cao, Z. Wu, Y. Su, and Z. Xu. Aircraft flight characteristics in icing conditions. Progress in Aerospace Sciences, 74, (2015), pp. 62–80.
L. Huang, Z. Liu, Y. Liu, Y. Gou, and L.Wang. Effect of contact angle on water droplet freezing process on a cold flat surface. Experimental Thermal and Fluid Science, 40, (2012), pp. 74–80.
Y. Pan, K. Shi, X. Duan, and G. F. Naterer. Experimental investigation of water droplet impact and freezing on micropatterned stainless steel surfaces with varying wettabilities. International Journal of Heat and Mass Transfer, 129, (2019), pp. 953–964.
H. Zhang, Z. Jin, M. Jiao, and Z. Yang. Experimental investigation of the impact and freezing processes of a water droplet on different cold concave surfaces. International Journal of Thermal Sciences, 132, (2018), pp. 498–508.
J. Ju, Z. Jin, H. Zhang, Z. Yang, and J. Zhang. The impact and freezing processes of a water droplet on different cold spherical surfaces. Experimental Thermal and Fluid Science, 96, (2018), pp. 430–440.
G. A. Satunkin. Determination of growth angles, wetting angles, interfacial tensions and capillary constant values of melts. Journal of Crystal Growth, 255, (2003), pp. 170–189.
W. W. Schultz, M. G. Worster, and D. M. Anderson. Solidifying sessile water droplets. In Interactive Dynamics of Convection and Solidification, Springer, Dordrecht, (2001), pp. 209–226,
A. Virozub, I. G. Rasin, and S. Brandon. Revisiting the constant growth angle: Estimation and verification via rigorous thermal modeling. Journal of Crystal Growth, 310, (2008), pp. 5416–5422.
T. V. Vu, G. Tryggvason, S. Homma, and J. C. Wells. Numerical investigations of drop solidification on a cold plate in the presence of volume change. International Journal of Multiphase Flow, 76, (2015), pp. 73–85.
C. Zhang, H. Zhang, W. Fang, Y. Zhao, and C. Yang. Axisymmetric lattice Boltzmann model for simulating the freezing process of a sessile water droplet with volume change. Physical Review E, 101, (2020).
H. Shetabivash, A. Dolatabadi, and M. Paraschivoiu. A multiple level-set approach for modelling containerless freezing process. Journal of Computational Physics, 415, (2020).
T. V. Vu and Q. H. Luu. Containerless solidification of a droplet under forced convection. International Journal of Heat and Mass Transfer, 143, (2019).
T. V. Vu, C. T. Nguyen, and D. T. Khanh. Direct numerical study of a molten metal drop solidifying on a cold plate with different wettability. Metals, 8, (2018).
V. N. Duy and T. V. Vu. A numerical study of a liquid drop solidifying on a vertical cold wall. International Journal of Heat and Mass Transfer, 127, (2018), pp. 302–312.
T. V. Vu. Fully resolved simulations of drop solidification under forced convection. International Journal of Heat and Mass Transfer, 122, (2018), pp. 252–263.
T. V. Vu, K. V. Dao, and B. D. Pham. Numerical simulation of the freezing process of a water drop attached to a cold plate. Journal of Mechanical Science and Technology, 32, (2018), pp. 2119–2126.
T. V. Vu. Deformation and breakup of a pendant drop with solidification. International Journal of Heat and Mass Transfer, 122, (2018), pp. 341–353.
T. Driessen, R. Jeurissen, H.Wijshoff, F. Toschi, and D. Lohse. Stability of viscous long liquid filaments. Physics of Fluids, 25, (2013).
A. Dziedzic, M. Nakrani, B. Ezra, M. Syed, S. Popinet, and S. Afkhami. Breakup of finite-size liquid filaments: Transition from no-breakup to breakup including substrate effects?. The European Physical Journal E, 42, (2019).
N. X. Ho, T. V. Vu, V. T. Nguyen, C. T. Nguyen, and H. V. Vu.Anumerical study of liquid compound filament contraction. Physics of Fluids, 33, (2021).
S. Hansen, G. W. M. Peters, and H. E. H. Meijer. The effect of surfactant on the stability of a fluid filament embedded in a viscous fluid. Journal of Fluid Mechanics, 382, (1999), pp. 331–349.
Y. Su, B. Palacios, and R. Zenit. Coiling of a viscoelastic fluid filament. Physical Review Fluids, 6, (2021).
X. Zhang. Dynamics of growth and breakup of viscous pendant drops into air. Journal of Colloid and Interface Science, 212, (1999), pp. 107–122.
T. V. Vu, S. Homma, J. C. Wells, H. Takakura, and G. Tryggvason. Numerical simulation of formation and breakup of a three-fluid compound jet. Journal of Fluid Science and Technology, 6, (2), (2011), pp. 252–263.
T. V. Vu, J. C. Wells, H. Takakura, S. Homma, and G. Tryggvason. Numerical calculations of pattern formation of compound drops detaching from a compound jet in a coflowing immiscible fluid. Journal of Chemical Engineering of Japan, 45, (9), (2012), pp. 721–726.
Cults. Identify and correct 3D printing problems.
K. Paraskevoudis, P. Karayannis, and E. P. Koumoulos. Real-time 3D printing remote defect detection (stringing) with computer vision and artificial intelligence. Processes, 8, (2020).
W. Oropallo and L. A. Piegl. Ten challenges in 3D printing. Engineering with Computers, 32, (2015), pp. 135–148.
T. V. Vu, A. V. Truong, N. T. B. Hoang, and D. K. Tran. Numerical investigations of solidification around a circular cylinder under forced convection. Journal of Mechanical Science and Technology, 30, (2016), pp. 5019–5028.
T. V. Vu and J. C. Wells. Numerical simulations of solidification around two tandemlyarranged circular cylinders under forced convection. International Journal of Multiphase Flow, 89, (2017), pp. 331–344.
T. V. Vu, L. V. Vu, B. D. Pham, and Q. H. Luu. Numerical investigation of dynamic behavior of a compound drop in shear flow. Journal of Mechanical Science and Technology, 32, (2018), pp. 2111–2117.
B. D. Pham, T. V. Vu, C. T. Nguyen, H. D. Nguyen, and V. T. Nguyen. Numerical study of collision modes of multi-core compound droplets in simple shear flow. Journal of Mechanical Science and Technology, 34, (2020), pp. 2055–2066.
N. X. Ho, T. V. Vu, and B. D. Pham. A numerical study of a liquid compound drop solidifying on a horizontal surface. International Journal of Heat and Mass Transfer, 165, (2021).
G. Tryggvason, B. Bunner, A. Esmaeeli, D. Juric, N. Al-Rawahi, W. Tauber, J. Han, S. Nas, and Y.-J. Jan. A front-tracking method for the computations of multiphase flow. Journal of Computational Physics, 169, (2001), pp. 708–759.
T. V. Vu, G. Tryggvason, S. Homma, J. C. Wells, and H. Takakura. A front-tracking method for three-phase computations of solidification with volume change. Journal of Chemical Engineering of Japan, 46, (11), (2013), pp. 726–731.
T.-V. Vu, T. V. Vu, C. T. Nguyen, and P. H. Pham. Deformation and breakup of a double-core compound droplet in an axisymmetric channel. International Journal of Heat and Mass Transfer, 135, (2019), pp. 796–810.
T. V. Vu. Three-phase computation of solidification in an open horizontal circular cylinder. International Journal of Heat and Mass Transfer, 111, (2017), pp. 398–409.
A. G. Marín, O. R. Enríquez, P. Brunet, P. Colinet, and J. H. Snoeijer. Universality of tip singularity formation in freezing water drops. Physical Review Letters, 113, (2014).
X. Zhang, X. Wu, and J. Min. Freezing and melting of a sessile water droplet on a horizontal cold plate. Experimental Thermal and Fluid Science, 88, (2017), pp. 1–7.
Downloads
Published
How to Cite
Issue
Section
License

This work is licensed under a Creative Commons Attribution-ShareAlike 4.0 International License.
Funding data
-
National Foundation for Science and Technology Development
Grant numbers 107.03-2019.307 -
Quỹ Đổi mới sáng tạo Vingroup
Grant numbers VINIF.2020.TS.140









