Convolutional neural network for homogenization of particulate composite materials based on finite element data

Tien-Thinh Le; Quoc Dat Ha; Huan Thanh Duong

doi:10.15625/0866-7136/22319

Author affiliations

Authors

Tien-Thinh Le Faculty of Mechanical Engineering and Mechatronics, PHENIKAA University, Yen Nghia, Ha Dong, Hanoi 12116, Vietnam https://orcid.org/0000-0002-1603-5000
Quoc Dat Ha Vietnam Petroleum Institute (VPI), 167 Trung Kinh, Cau Giay, Hanoi, Vietnam https://orcid.org/0000-0002-6809-4870
Huan Thanh Duong Faculty of Engineering, Vietnam National University of Agriculture, Trau Quy, Gia Lam, Hanoi, Vietnam https://orcid.org/0000-0002-2045-7759

DOI:

https://doi.org/10.15625/0866-7136/22319

Keywords:

convolutional neural network, finite element simulation, multiscale homogenization, particulate composites

Abstract

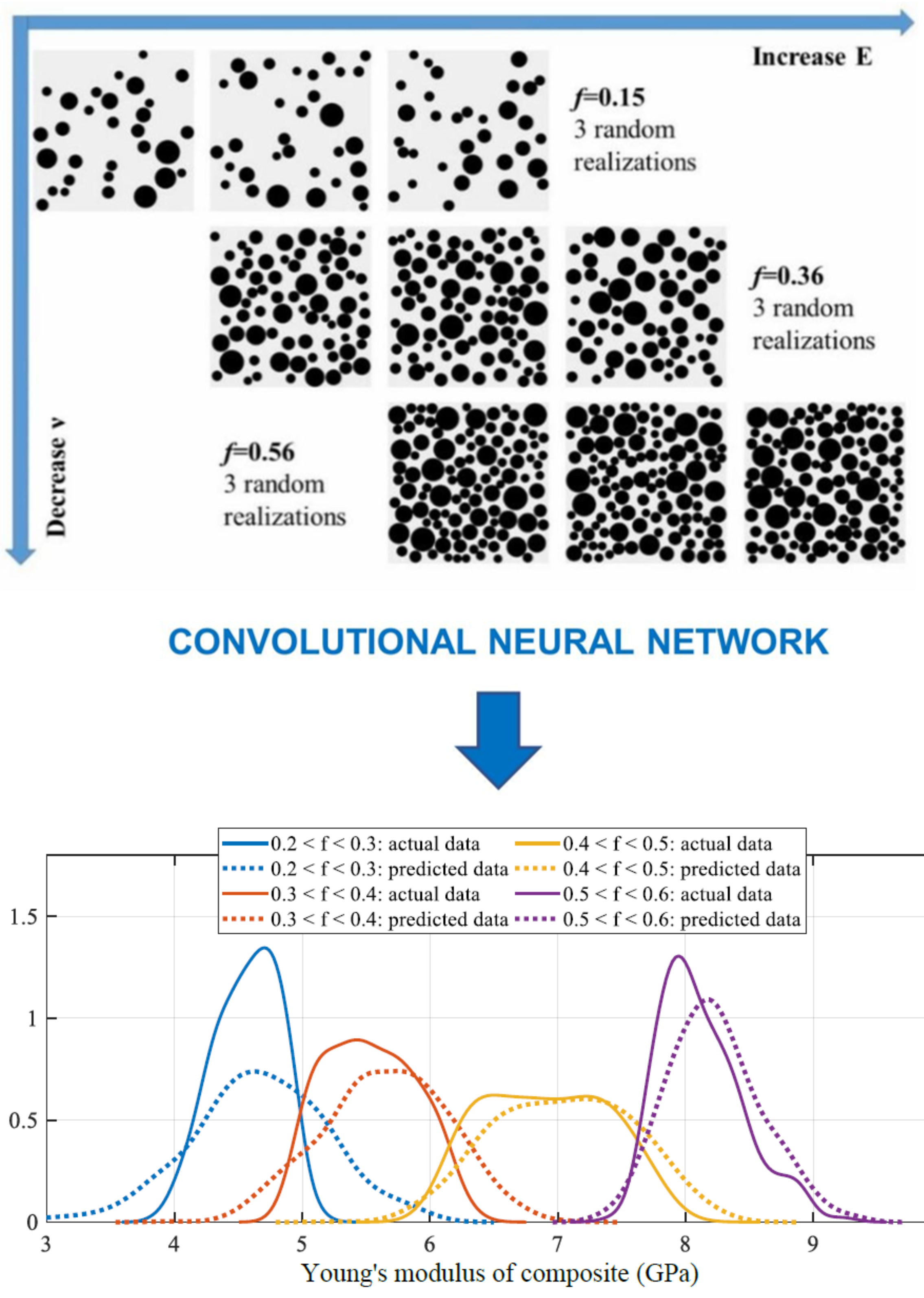
This study develops a convolutional neural network model to predict the apparent mechanical properties of particulate composite materials based on finite element data. The particulate composite material is considered with random inclusions in size and position. The datasets for training and testing processes are generated by using a validated finite element simulation. Various parametric studies are then investigated, including model efficiency and uncertainty propagation. Moreover, the influence of the constituents and microstructure is numerically revealed based on the proposed convolutional neural network model. It is shown that the developed convolutional neural network model is capable of capturing the microstructural features and provides accurate predictions of apparent mechanical properties of particulate composite materials.

Downloads

References

[1] J. W. Ju and K. Yanase. Micromechanics and effective elastic moduli of particle-reinforced composites with near-field particle interactions. Acta Mechanica, 215, (2010), pp. 135–153. https://doi.org/10.1007/s00707-010-0337-2.

[2] J. C. Smith. Experimental values for the elastic constants of a particulate-filled glassy polymer. Journal of Research of the National Bureau of Standards Section A: Physics and Chemistry, 80A, (1976). https://doi.org/10.6028/jres.080a.008.

[3] B. Raju, S. R. Hiremath, and D. Roy Mahapatra. A review of micromechanics based models for effective elastic properties of reinforced polymer matrix composites. Composite Structures, 204, (2018), pp. 607–619. https://doi.org/10.1016/j.compstruct.2018.07.125.

[4] M. Barral, G. Chatzigeorgiou, F. Meraghni, and R. Léon. Homogenization using modified Mori-Tanaka and TFA framework for elastoplastic-viscoelastic-viscoplastic composites: Theory and numerical validation. International Journal of Plasticity, 127, (2020). https://doi.org/10.1016/j.ijplas.2019.11.011.

[5] S. Kanaun. An efficient homogenization method for composite materials with elastoplastic components. International Journal of Engineering Science, 57, (2012), pp. 36–49. https://doi.org/10.1016/j.ijengsci.2012.04.005.

[6] X. Peng and J. Cao. A dual homogenization and finite element approach for material characterization of textile composites. Composites Part B: Engineering, 33, (2002), pp. 45–56. https://doi.org/10.1016/s1359-8368(01)00052-x.

[7] L. Taut and V. Monchiet. Numerical homogenization with FFT method for elastic composites with spring-type interfaces. Composite Structures, 305, (2023). https://doi.org/10.1016/j.compstruct.2022.116426.

[8] J. Jiang, J. Wu, Q. Chen, G. Chatzigeorgiou, and F. Meraghni. Physically informed deep homogenization neural network for unidirectional multiphase/multi-inclusion thermoconductive composites. Computer Methods in Applied Mechanics and Engineering, 409, (2023). https://doi.org/10.1016/j.cma.2023.115972.

[9] F. Kibrete, T. Trzepieciński, H. S. Gebremedhen, and D. E. Woldemichael. Artificial intelligence in predicting mechanical properties of composite materials. Journal of Composites Science, 7, (2023). https://doi.org/10.3390/jcs7090364.

[10] H. R. Bayat, B. Mustaq, and A. Vötterl. Predictive residual stress analysis in gear units: an artificial intelligence approach based on finite element data. Advances in Mechanical Engineering, 16, (2024). https://doi.org/10.1177/16878132241290948.

[11] N. Altinkok and R. Koker. Neural network approach to prediction of bending strength and hardening behaviour of particulate reinforced (Al–Si–Mg)-aluminium matrix composites. Materials & Design, 25, (2004), pp. 595–602. https://doi.org/10.1016/j.matdes.2004.02.014.

[12] R. Koker, N. Altinkok, and A. Demir. Neural network based prediction of mechanical properties of particulate reinforced metal matrix composites using various training algorithms. Materials & Design, 28, (2007), pp. 616–627. https://doi.org/10.1016/j.matdes.2005.07.021.

[13] X. Li, Y. Zhang, H. Zhao, C. Burkhart, L. C. Brinson, and W. Chen. A transfer learning approach for microstructure reconstruction and structure-property predictions. Scientific Reports, 8, (2018). https://doi.org/10.1038/s41598-018-31571-7.

[14] A. Henkes, I. Caylak, and R. Mahnken. A deep learning driven uncertain full-field homogenization method. PAMM, 20, (2021). https://doi.org/10.1002/pamm.202000180.

[15] W. Wang, Y. Zhao, and Y. Li. Ensemble machine learning for predicting the homogenized elastic properties of unidirectional composites: A SHAP-based interpretability analysis. Acta Mechanica Sinica, 40, (2023). https://doi.org/10.1007/s10409-023-23301-x.

[16] Y. Wang, C. Soutis, D. Ando, Y. Sutou, and F. Narita. Application of deep neural network learning in composites design. European Journal of Materials, 2, (2022), pp. 117–170. https://doi.org/10.1080/26889277.2022.2053302.

[17] H. Ahmadi Moghaddam and P. Mertiny. Stochastic finite element analysis framework for modelling mechanical properties of particulate modified polymer composites. Materials, 12, (2019). https://doi.org/10.3390/ma12172777.

[18] C. Rao and Y. Liu. Three-dimensional convolutional neural network (3D-CNN) for heterogeneous material homogenization. Computational Materials Science, 184, (2020). https://doi.org/10.1016/j.commatsci.2020.109850.

[19] A. Valishin and N. Beriachvili. Applying neural networks to analyse the properties and structure of composite materials. In S. Kovacˇevic´ and K. Kamyshev, editors, E3S Web of Conferences, EDP Sciences, Vol. 376, (2023). https://doi.org/10.1051/e3sconf/202337601041.