A design of tuned mass damper with piezoelectric stack energy harvester and two-stage force amplification frame

Author affiliations

Authors

  • Nguyen Anh Ngoc \(^1\) University of Transport and Communications, Hanoi, Vietnam https://orcid.org/0000-0001-7322-3940
  • Tong Duc Nang \(^2\) Hanoi University of Civil Engineering, Hanoi, Vietnam
  • Vu Anh Tuan \(^2\) Hanoi University of Civil Engineering, Hanoi, Vietnam
  • Nguyen Dong Anh \(^3\) Institute of Mechanics, Vietnam Academy of Science and Technology, Hanoi, Vietnam
    \(^4\) University of Engineering and Technology, VNU, Vietnam     https://orcid.org/0000-0002-8338-4497
  • La Duc Viet \(^3\) Institute of Mechanics, Vietnam Academy of Science and Technology, Hanoi, Vietnam
    \(^4\) University of Engineering and Technology, VNU, Vietnam     https://orcid.org/0000-0002-8600-2175
  • Tran Tuan Anh \(^5\) Thuyloi University, Hanoi, Vietnam
  • Nguyen Ngoc Linh \(^5\) Thuyloi University, Hanoi, Vietnam https://orcid.org/0000-0002-6724-462X

DOI:

https://doi.org/10.15625/0866-7136/21026

Keywords:

tuned mass damper, piezo stack energy harvester, two-stage force amplification frame

Abstract

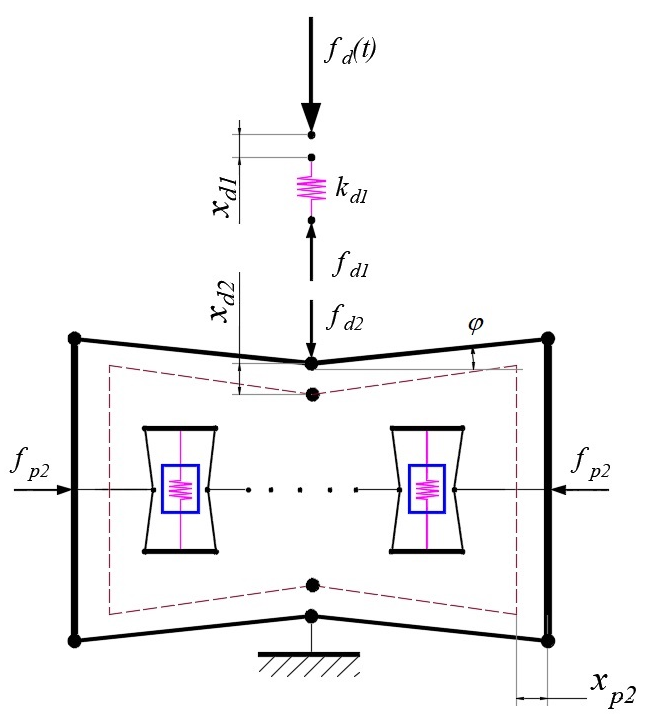
The paper deals with a novel tuned mass damper (TMD) with an energy harvester consisting of a combination of piezo stacks and two-stage force amplification frames connected in series with TMD springs (TMD-2sPSFAFs). The governing equations of 2sPSFAF are established first, followed by those of TMD-2sPSFAF. It will be demonstrated that the reduced order model of the series combination of 2sPSFAF and TMD spring is an equivalent piezo stack energy harvester. Using the optimal results according to the fixed point theory, the conditions for selecting stiffnesses of piezo stacks and TMD spring are obtained. Next, a numerical examination of the electromechanical system reveals that the voltage amplitude curve has a fixed point independent of TMD spring stiffness. Furthermore, an effective stiffness of the TMD spring would be found to ensure that the peaks of mechanical magnification and voltage amplitude curves are of equal heights.

Downloads

Download data is not yet available.

References

[1] A. Erturk and D. J. Inman. Piezoelectric energy harvesting. Wiley, (2011). https://doi.org/10.1002/9781119991151.

[2] M. Goldfarb and N. Celanovic. Modeling piezoelectric stack actuators for control of micro-manipulation. IEEE Control Systems Magazine, 17, (3), (1997), pp. 69–79.

[3] F. Qian, T.-B. Xu, and L. Zuo. Design, optimization, modeling and testing of a piezoelectric footwear energy harvester. Energy Conversion and Management, 171, (2018), pp. 1352–1364. https://doi.org/10.1016/j.enconman.2018.06.069.

[4] X. Jiang, Y. Li, J. Li, J. Wang, and J. Yao. Piezoelectric energy harvesting from traffic-induced pavement vibrations. Journal of Renewable and Sustainable Energy, 6, (2014). https://doi.org/10.1063/1.4891169.

[5] W. Hendrowati, H. L. Guntur, and I. N. Sutantra. Design, modeling and analysis of implementing a multilayer piezoelectric vibration energy harvesting mechanism in the vehicle suspension. Engineering, 04, (11), (2012), pp. 728–738. https://doi.org/10.4236/eng.2012.411094.

[6] J. Wang, Z. Shi, H. Xiang, and G. Song. Modeling on energy harvesting from a railway system using piezoelectric transducers. Smart Materials and Structures, 24, (2015), p. 105017. https://doi.org/10.1088/0964-1726/24/10/105017.

[7] Y.-A. Lai, J.-Y. Kim, C.-S. W. Yang, and L.-L. Chung. A low-cost and efficient d33-mode piezoelectric tuned mass damper with simultaneously optimized electrical and mechanical tuning. Journal of Intelligent Material Systems and Structures, 32, (2020), pp. 678–696. https://doi.org/10.1177/1045389x20966056.

[8] Y. Wang, W. Chen, and P. Guzman. Piezoelectric stack energy harvesting with a force amplification frame: Modeling and experiment. Journal of Intelligent Material Systems and Structures, 27, (2016), pp. 2324–2332. https://doi.org/10.1177/1045389x16629568.

[9] L. Wang, S. Chen, W. Zhou, T.-B. Xu, and L. Zuo. Piezoelectric vibration energy harvester with two-stage force amplification. Journal of Intelligent Material Systems and Structures, 28, (2016), pp. 1175–1187. https://doi.org/10.1177/1045389x16667551.

[10] N. N. Linh, V. A. Tuan, N. V. Tuan, and N. D. Anh. Response analysis of undamped primary system subjected to base excitation with a dynamic vibration absorber integrated with a piezoelectric stack energy harvester. Vietnam Journal of Mechanics, 44, (2022), pp. 490–499. https://doi.org/10.15625/0866-7136/17948.

[11] N. N. Linh, N. D. Anh, L. D. Viet, N. A. Ngoc, V. A. Tuan, T. D. Nang, and N. V. Manh. Patent Title: Tuned mass damper with integrated vibrating piezoelectric energy harvester. Intellectual Property Office of Vietnam, Patent number: 39054, Application Number: 1-2022-02620, Publication Number: 1/088043 A, Publication date: 26 July (in Vietnamese), (2024). https://ipvietnam.gov.vn/documents/20182/1630076/39054.pdf/c254ef2a-e0ac-491f-ba4c- 6709cda1b0a2.

[12] N. N. Linh. Series combination models of piezoelectric energy harvesters with spring and damper. In the 11th National Conference on Mechanics, Vol. 2, (2022).

[13] N. N. Linh and N. D. Anh. A novel configuration of tuned mass damper with energy harvester of piezoelectric stack and force amplification frame. In Proceedings of the 7th International Conference on Engineering Mechanics and Automation, Publishing House for Science and Technology, ICEMA 2023, (2023). https://doi.org/10.15625/vap.2023.0146.

[14] N. D. Anh, V. A. Tuan, P. M. Thang, and N. N. Linh. Extension of the fixed point theory to tuned mass dampers with piezoelectric stack energy harvester. Journal of Sound and Vibration, 581, (2024). https://doi.org/10.1016/j.jsv.2024.118411.

[15] J. D. Hartog. Mechanical vibrations. Dover, New York, (1985).

[16] J. Connor and S. Laflamme. Structural motion engineering. Springer International Publishing, Switzerland, (2014).

Downloads

Published

30-06-2024

Issue

Vol. 46 No. 3 (2024)

Section

Research Article

Categories

License

Creative Commons License

This work is licensed under a Creative Commons Attribution-ShareAlike 4.0 International License.

Crossref
Scopus
Google Scholar
Europe PMC

Most read articles by the same author(s)

1 2 3 4 5 > >>