Dynamic response of arbitrary double-curved shells by meridian curve digitalization
Author affiliations
DOI:
https://doi.org/10.15625/0866-7136/17305Keywords:
closed loop multibody system, electromechanical system, singularity-free, constrained stabilization, post-adjusting techniqueAbstract
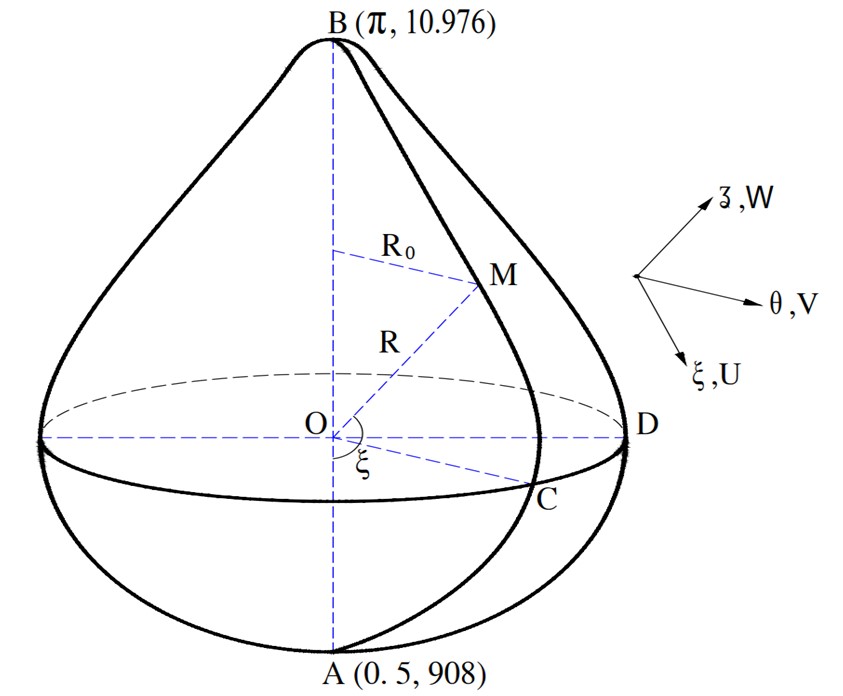
For the resulting equation of double-curved shells, which is formed by revolution of an arbitrary in-plane meridian curve and cannot be represented analytically, there exists no analytical approach to problem setting and solution. This paper presents the digitalization of the meridian curve in the polar coordinate system, which forms double number series. The double number series then can be approximated by an interpolation function so that calculations can be performed in a similar methodology for an explicit function. Digitalization enables the input parameters in the form of interpolation functions. Procedures for the proposed selection of solution forms, formation of the kinetic equation, and computation of coefficients for the kinetic equation from on the interpolation and explicit functions are presented in the paper. The final solution is obtained by using the program Mathematica 7.0 to solve the system of nonlinear differential equations. Assessment of the dynamic response of the double-curved shell, especially responses with chaotic motion, is also presented in the paper.
Downloads
References
https://news.zing.vn/8-khoi-thap-nuoc-be-tong-khong-lo-giua-sai-gon post592538.html.
V. Q. Hien, T. I. Thinh, N. M. Cuong, and P. N. Thanh. Free vibration analysis of joined composite conical-conical-conical shells containing fluid. Vietnam Journal of Science and Technology, 54, (2016).
M. Shakouri and M. A. Kouchakzadeh. Free vibration analysis of joined conical shells: Analytical and experimental study. Thin-Walled Structures, 85, (2014), pp. 350–358.
K. Xie, M. Chen, and Z. Li. An analytic method for free and forced vibration analysis of stepped conical shells with arbitrary boundary conditions. Thin-Walled Structures, 111, (2017), pp. 126–137.
B. P. Patel, M. Ganapathi, and S. Kamat. Free vibration characteristics of laminated composite joined conical-cylindrical shells. Journal of Sound and Vibration, 237, (2000), pp. 920–930.
Y. Qu, Y. Chen, X. Long, H. Hua, and G. Meng. A variational method for free vibration analysis of joined cylindrical-conical shells. Journal of Vibration and Control, 19, (2012), pp. 2319–2334.
Y. Kerboua and A. A. Lakis. Numerical model to analyze the aerodynamic behavior of a combined conical–cylindrical shell. Aerospace Science and Technology, 58, (2016), pp. 601–617.
Y. Kerboua and A. A. Lakis. Dynamic behavior of a rocket filled with liquid. Universal Journal of Aeronautical & Aerospace Sciences, 2, (2014), pp. 55–79.
D. Chronopoulos, M. Ichchou, B. Troclet, and O. Bareille. Predicting the broadband response of a layered cone-cylinder-cone shell. Composite Structures, 107, (2014), pp. 149–159.
M. Chen, K. Xie, J.Wei, and N. Deng. An analytical substructure method for the analysis of vibration characteristics on conical-cylindrical-spherical combined shells in vacuum. Inter-noise, (2014).
K. Xie, M. Chen, and Z. Li. Free and forced vibration analysis of ring-stiffened conical– cylindrical–spherical shells through a semi-Analytic method. Journal of Vibration and Acoustics, 139, (2017).
M. Moonesun, F. Ghasemzadeh, Y. Korol, V. Nikrasov, A. Yastreba, A. Ursolov, and A. Mahdian. Technical notes on the near surface experiments of submerged submarine. International Journal of Maritime Technology, 5, (2016), pp. 41–54.
G. A. Korn and T. M. Korn. Mathematica handbook, p. 519. McGrow - Hill Book Company, (1968).
Downloads
Published
How to Cite
Issue
Section
License

This work is licensed under a Creative Commons Attribution-ShareAlike 4.0 International License.









