Dynamic modelling and singularity-free simulation of closed loop multibody system driven by electric motors
Author affiliations
DOI:
https://doi.org/10.15625/0866-7136/16977Keywords:
closed loop multibody system, electromechanical system, singularity-free, constrained stabilization, post-adjusting techniqueAbstract
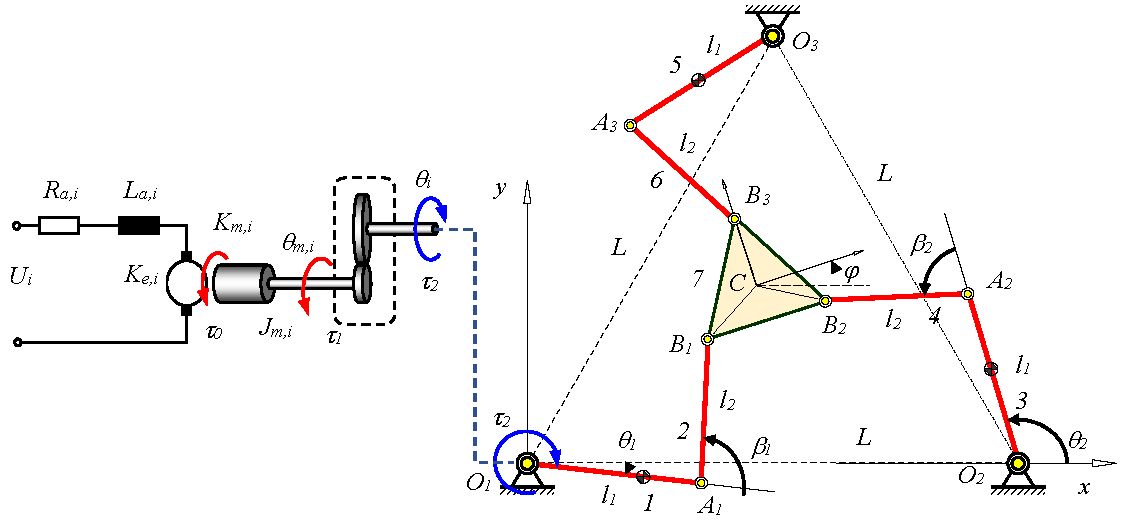
This paper presents the dynamic model and singularity-free simulation of electromechanical systems including closed loop multibody systems, massless gear transmission and electric motors. The dynamic model of these systems is established in matrix form and written in a Differential-Algebraic Equations form by applying the Lagrangian equation with multipliers and substructure method. Moreover, this paper deals with two difficult issues in the simulation of closed-loop multibody systems which are to overcome smoothly the singular configurations and to stabilize the constrained equations due to accumulated errors. The singularity-free simulation is solved by using null-space of Jacobian matrix to eliminate the constraint forces – Lagrangian multipliers in equations of motion. The drift in the constraint equation during simulation is restricted by a combination of Baumgarte’s stabilization and post-adjusting technique. Some numerical experiments are carried out to the planar 3RRR parallel manipulator driven by electric motors. Simulation results confirm the effectiveness of the proposed approach in overcoming the singular configurations and in stabilization of the constraint.
Downloads
Metrics
References
A. A. Shabana. Dynamics of multibody systems. Cambridge University Press, (2013). DOI: https://doi.org/10.1017/CBO9781107337213
T. R. Kane and D. A. Levinson. Dynamics, theory and applications. McGraw Hill, (1985).
J. Wittenburg. General multibody systems. Springer, (2008).
F. M. L. Amirouche and F. M. L. Amirouche. Fundamentals of multibody dynamics: Theory and applications. Springer, (2006).
R. M. Murray, Z. Li, and S. S. Sastry. A mathematical introduction to robotic manipulation. CRC Press, (2017). DOI: https://doi.org/10.1201/9781315136370
R. Von Schwerin. Multibody system simulation: numerical methods, algorithms, and software, Vol. 7. Springer Science & Business Media, (1999).
F. C. Moon. Applied dynamics: with applications to multibody and mechatronic systems. JohnWiley & Sons, (2008).
H. Gattringer and J. Gerstmayr. Multibody system dynamics, robotics and control. Springer Vienna, (2013). DOI: https://doi.org/10.1007/978-3-7091-1289-2
R. N. Jazar. Advanced dynamics. Wiley, (2011). DOI: https://doi.org/10.1002/9780470950029
W. Schiehlen. Multibody systems handbook, Vol. 6. Springer Berlin Heidelberg, (1990). DOI: https://doi.org/10.1007/978-3-642-50995-7
N. V. Khang. Dynamics of multibody systems. Science and Technology Publishing House, Hanoi, (2007).
L.-W. Tsai. Robot analysis: the mechanics of serial and parallel manipulators. John Wiley & Sons, (1999).
P. E. Nikravesh. Computer-aided analysis of mechanical systems. Prentice-Hall, Inc., (1988).
J. Angeles. Fundamentals of robotic mechanical systems, Vol. 2. Springer, (2002).
J. G. De Jalon and E. Bayo. Kinematic and dynamic simulation of multibody systems: the real-time challenge. Springer Science & Business Media, (2012).
J. P. Merlet. Fundamentals of mechanics of robotic manipulation, Vol. 27. Springer Science & Business Media, (2013).
L. Sciavicco and B. Siciliano. Modelling and control of robot manipulators. Springer Science & Business Media, (2012).
J.-P. Merlet. Parallel robots, Vol. 128. Springer Science & Business Media, (2005). DOI: https://doi.org/10.1115/1.2121740
H. D. Taghirad. Parallel robots. CRC Press, (2013). DOI: https://doi.org/10.1201/b16096
M. W. Spong, S. Hutchinson, M. Vidyasagar, et al. Robot modeling and control, Vol. 3. Wiley New York, (2006).
P. E. Nikravesh. Some methods for dynamic analysis of constrained mechanical systems: a survey. In Computer Aided Analysis and Optimization of Mechanical System Dynamics. Springer Berlin Heidelberg, (1984), pp. 351–368. DOI: https://doi.org/10.1007/978-3-642-52465-3_14
R. A.Wehage and E. J. Haug. Generalized coordinate partitioning for dimension reduction in analysis of constrained dynamic systems. Journal of Mechanical Design, 104, (1982), pp. 247–255. DOI: https://doi.org/10.1115/1.3256318
S. K. Ider and F. M. L. Amirouche. Coordinate reduction in the dynamics of constrained multibody systems—a new approach. Journal of Applied Mechanics, 55, (1988), pp. 899–904. DOI: https://doi.org/10.1115/1.3173739
F. M. L. Amirouche and C.-W. Tung. Regularization and stability of the constraints in the dynamics of multibody systems. Nonlinear Dynamics, 1, (1990), pp. 459–475. DOI: https://doi.org/10.1007/BF01856949
E. Bayo and R. Ledesma. Augmented lagrangian and mass-orthogonal projection methods for constrained multibody dynamics. Nonlinear Dynamics, 9, (1996), pp. 113–130. DOI: https://doi.org/10.1007/BF01833296
E. Bayo, J. G. D. Jalon, and M. A. Serna. A modified lagrangian formulation for the dynamic analysis of constrained mechanical systems. Computer Methods in Applied Mechanics and Engineering, 71, (1988), pp. 183–195. DOI: https://doi.org/10.1016/0045-7825(88)90085-0
J. C. G. Orden and R. A. Ortega. A conservative augmented Lagrangian algorithm for the dynamics of constrained mechanical systems. In III European Conference on Computational Mechanics. Springer Netherlands, pp. 619–619.
A. Laulusa and O. A. Bauchau. Review of classical approaches for constraint enforcement in multibody systems. Journal of Computational and Nonlinear Dynamics, 3, (2007). DOI: https://doi.org/10.1115/1.2803257
J. Baumgarte. Stabilization of constraints and integrals of motion in dynamical systems. Computer Methods in Applied Mechanics and Engineering, 1, (1972), pp. 1–16. DOI: https://doi.org/10.1016/0045-7825(72)90018-7
S.-T. Lin and J.-N. Huang. Stabilization of Baumgarte’s method using the Runge-Kutta approach. Journal of Mechanical Design, 124, (2002), pp. 633–641. DOI: https://doi.org/10.1115/1.1519277
Z. Terze, D. Lefeber, and O. Mufti´c. Null space integration method for constrained multibody systems with no constraint violation. Multibody System Dynamics, 6, (3), (2001), pp. 229–243. DOI: https://doi.org/10.1023/A:1012090712309
N. V. Khang. Kronecker product and a new matrix form of Lagrangian equations with multipliers for constrained multibody systems. Mechanics Research Communications, 38, (2011), pp. 294–299. DOI: https://doi.org/10.1016/j.mechrescom.2011.04.004
N. Q. Hoang, V. D. Vuong, and N. V. Quyen. Modeling and Model-Based Controller Design for 3RRR Planar Parallel Robots Driven by DC Motors in Joint Space. In the 4th International Conference on Engineering Mechanics and Automation (ICEMA 4), Vol. 4, (2016), pp. 114–123.
J. Moreno-Valenzuela, R. Campa, and V. Santibanez. Model-based control of a class of voltage-driven robot manipulators with non-passive dynamics. Computers & Electrical Engineering, 39, (2013), pp. 2086–2099. DOI: https://doi.org/10.1016/j.compeleceng.2013.06.006
M. M. Fateh. On the voltage-based control of robot manipulators. International Journal of Control, Automation, and Systems, 6, (5), (2008), pp. 702–712.
W. Blajer, W. Schiehlen, and W. Schirm. A projective criterion to the coordinate partitioning method for multibody dynamics. Archive of Applied Mechanics, 64, (1994), pp. 86–98. DOI: https://doi.org/10.1007/BF00789100
Y. Nakamura. Advanced robotics: redundancy and optimization. Addison-Wesley Longman Publishing Co., Inc., (1990).
C. Meyer. Matrix analysis and applied linear algebra. SIAM, (2000). DOI: https://doi.org/10.1137/1.9780898719512
D. J. Braun and M. Goldfarb. Eliminating constraint drift in the numerical simulation of constrained dynamical systems. Computer Methods in Applied Mechanics and Engineering, 198, (2009), pp. 3151–3160. DOI: https://doi.org/10.1016/j.cma.2009.05.013
F.-C. Tseng, Z.-D. Ma, and G. M. Hulbert. Efficient numerical solution of constrained multibody dynamics systems. Computer Methods in Applied Mechanics and Engineering, 192, (2003), pp. 439–472. DOI: https://doi.org/10.1016/S0045-7825(02)00521-2
E. Bayo and A. Avello. Singularity-free augmented Lagrangian algorithms for constrained multibody dynamics. Nonlinear Dynamics, 5, (1994), pp. 209–231. DOI: https://doi.org/10.1007/BF00045677
O. A. Bauchau and A. Laulusa. Review of contemporary approaches for constraint enforcement in multibody systems. Journal of Computational and Nonlinear Dynamics, 3, (2007). DOI: https://doi.org/10.1115/1.2803258
W. Blajer. Elimination of constraint violation and accuracy aspects in numerical simulation of multibody systems. Multibody System Dynamics, 7, (3), (2002), pp. 265–284. DOI: https://doi.org/10.1023/A:1015285428885
E. Eich. Convergence results for a coordinate projection method applied to mechanical systems with algebraic constraints. SIAM Journal on Numerical Analysis, 30, (1993), pp. 1467–1482. DOI: https://doi.org/10.1137/0730076
S. Yoon, R. M. Howe, and D. T. Greenwood. Geometric elimination of constraint violations in numerical simulation of Lagrangian equations. Journal of Mechanical Design, 116, (1994), pp. 1058–1064. DOI: https://doi.org/10.1115/1.2919487
S. K. Ider and F. M. L. Amirouche. Numerical stability of the constraints near singular positions in the dynamics of multibody systems. Computers & Structures, 33, (1989), pp. 129–137. DOI: https://doi.org/10.1016/0045-7949(89)90135-1
S. Liu, Z. cheng Qiu, and X. min Zhang. Singularity and path-planning with the working mode conversion of a 3-DOF 3-RRR planar parallel manipulator. Mechanism and Machine Theory, 107, (2017), pp. 166–182. DOI: https://doi.org/10.1016/j.mechmachtheory.2016.09.004
N. Q. Hoang and V. D. Vuong. Sliding mode control for a Planar parallel robot driven by electric motors in a task space. Journal of Computer Science and Cybernetics, 33, (2018), pp. 325–337. DOI: https://doi.org/10.15625/1813-9663/33/4/10339
T. D. Thanh, J. Kotlarski, B. Heimann, and T. Ortmaier. Dynamics identification of kinematically redundant parallel robots using the direct search method. Mechanism and Machine Theory, 55, (2012), pp. 104–121. DOI: https://doi.org/10.1016/j.mechmachtheory.2012.03.011
P. Flores, R. Pereira, M. Machado, and E. Seabra. Investigation on the baumgarte stabilization method for dynamic analysis of constrained multibody systems. In Proceedings of EUCOMES 08. Springer Netherlands, pp. 305–312. DOI: https://doi.org/10.1007/978-1-4020-8915-2_37
G.-P. Ostermeyer. On Baumgarte stabilization for differential algebraic equations. In Real-Time Integration Methods for Mechanical System Simulation. Springer Berlin Heidelberg, (1990), pp. 193–207. DOI: https://doi.org/10.1007/978-3-642-76159-1_10
Q. Yu and I.-M. Chen. A direct violation correction method in numerical simulation of constrained multibody systems. Computational Mechanics, 26, (2000), pp. 52–57. DOI: https://doi.org/10.1007/s004660000149
Downloads
Published
How to Cite
License
This work is licensed under a Creative Commons Attribution-ShareAlike 4.0 International License.
