Modeling of parallel manipulators with flexible links and joints driven by electric actuators
Author affiliations
DOI:
https://doi.org/10.15625/0866-7136/17944Keywords:
parallel robot manipulator, elastic links, elastic joints, modeling, numerical simulationAbstract
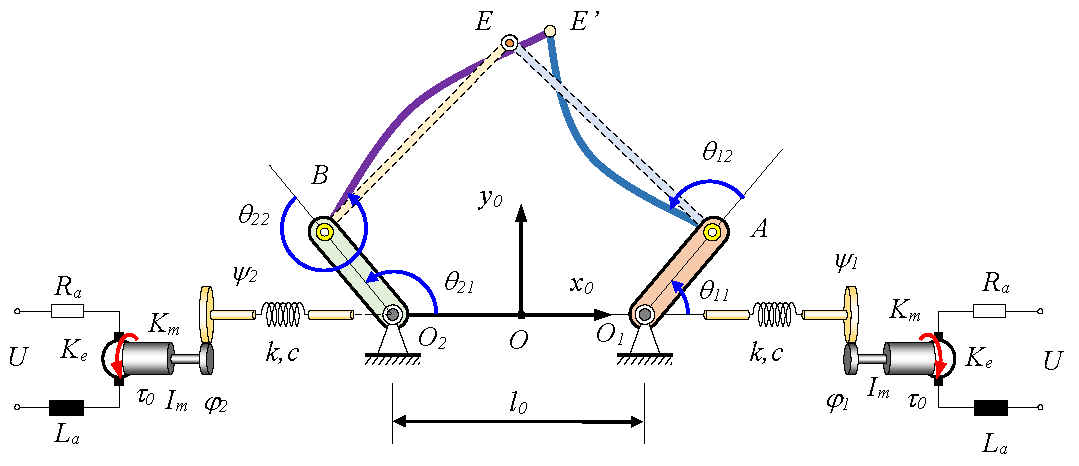
This paper presents the approach of building a mathematical model for a parallel robotic manipulator with flexible links and elastic joints. The links to the base are assumed to be rigid bodies, and the thin connecting rods are assumed to be flexible links. The elasticity of the transmission from the actuators to the transmission is modeled by a torsional spring and viscous damper. This is a mixed system of rigid bodies, spring, and flexible links. The deformation motion of the elastic link is approximated by shape functions similar to the finite element method. The differential equations of motion are established by combining the substructure method and the Lagrange equation of the 2nd kind for the serial multibody system. Based on the differential equation established for the parallel robot manipulator of five bars, numerical simulations were carried out to investigate the response of the system.
Downloads
References
A. A. Shabana. Multibody System Dynamics, 1, (2), (1997), pp. 189–222. DOI: https://doi.org/10.1023/A:1009773505418
S. K. Dwivedy and P. Eberhard. Dynamic analysis of flexible manipulators, a literature review. Mechanism and Machine Theory, 41, (2006), pp. 749–777. DOI: https://doi.org/10.1016/j.mechmachtheory.2006.01.014
K. Lochan, B. K. Roy, and B. Subudhi. A review on two-link flexible manipulators. Annual Reviews in Control, 42, (2016), pp. 346–367. DOI: https://doi.org/10.1016/j.arcontrol.2016.09.019
Y. Gao, F.-Y. Wang, and Z.-Q. Zhao. Flexible manipulators: Modeling, analysis and optimum design. Academic Press, (2012).
R. E. Valembois, P. Fisette, and J. C. Samin. Comparison of various techniques for modelling flexible beams in multibody dynamics. Nonlinear Dynamics, 12, (4), (1997), pp. 367–397. DOI: https://doi.org/10.1023/A:1008204330035
T. M.Wasfy and A. K. Noor. Computational strategies for flexible multibody systems. Applied Mechanics Reviews, 56, (2003), pp. 553–613. DOI: https://doi.org/10.1115/1.1590354
M. Benosman and G. Le Vey. Joint trajectory tracking for planar multi-link flexible manipulator: Simulation and experiment for a two-link flexible manipulator. In Proceedings 2002 IEEE International Conference on Robotics and Automation (Cat. No. 02CH37292), IEEE, Vol. 3, (2002), pp. 2461–2466.
R. Seifried. Dynamics of underactuated multibody systems. Springer International Publishing, (2014). DOI: https://doi.org/10.1007/978-3-319-01228-5
N. Q. Hoang. Effect of motion law on driving torque and oscillation of manipulators with flexible links. In the proceedings of 10th National Conference of Mechanics, Volume 2, Dynamics and Controls, (2017). (in Vietnamse).
D. C. Dat, N. V. Khang, N. Q. Hoang, and N. V. Quyen. Stability control of dynamical systems described by linear differential equations with time-periodic coefficients. In Advances in Asian Mechanism and Machine Science. Springer International Publishing, (2021), pp. 489–500. DOI: https://doi.org/10.1007/978-3-030-91892-7_46
C. A. My and D. X. Bien. New development of the dynamic modeling and the inverse dynamic analysis for flexible robot. International Journal of Advanced Robotic Systems, 17, (4), (2020). DOI: https://doi.org/10.1177/1729881420943341
S. Briot and W. Khalil. Dynamics of parallel robots: from rigid bodies to flexible elements. Mechanisms and machine science. Springer, Berlin, (2015). DOI: https://doi.org/10.1007/978-3-319-19788-3
N. V. Khang, N. S. Nam, and N. P. Dien. Modelling and model-based control of a four-bar mechanism with a flexible coupler link. In Robotics and Mechatronics. Springer International Publishing, (2019), pp. 67–81. DOI: https://doi.org/10.1007/978-3-030-17677-8_6
Q. Zhang, X. Fan, and X. Zhang. Dynamic analysis of planar 3-RRR flexible parallel robots with dynamic stiffening. Shock and Vibration, 2014, (2014), pp. 1–13. DOI: https://doi.org/10.1155/2014/370145
D. Zhaocai and Y. Yueqing. Dynamic modeling and inverse dynamic analysis of flexible parallel robots. International Journal of Advanced Robotic Systems, 5, (2008). DOI: https://doi.org/10.5772/5654
C. Zhengsheng, K. Minxiu, L. Ming, and Y. Wei. Dynamic modelling and trajectory tracking of parallel manipulator with flexible link. International Journal of Advanced Robotic Systems, 10, (2013). DOI: https://doi.org/10.5772/56765
S.-M. Kim. Lumped element modeling of a flexible manipulator system. IEEE/ASME Transactions on Mechatronics, 20, (2015), pp. 967–974. DOI: https://doi.org/10.1109/TMECH.2014.2327070
H. Cervantes-Culebro, J. E. Chong-Quero, E. A. Padilla-Garcia, and C. A. Cruz-Villar. Concurrent design of a 2 DOF five-bar parallel robot a hybrid design of rigid and flexible links. IEEE Access, 9, (2021), pp. 17450–17462. DOI: https://doi.org/10.1109/ACCESS.2021.3053250
Z.-C. Qiu. Adaptive nonlinear vibration control of a Cartesian flexible manipulator driven by a ballscrew mechanism. Mechanical Systems and Signal Processing, 30, (2012), pp. 248–266. DOI: https://doi.org/10.1016/j.ymssp.2012.01.002
M. Dadfarnia, N. Jalili, B. Xian, and D. M. Dawson. Lyapunov-based vibration control of translational Euler-Bernoulli beams using the stabilizing effect of beam damping mechanisms. Journal of Vibration and Control, 10, (2004), pp. 933–961. DOI: https://doi.org/10.1177/1077546304042070
H. Yang, H. Krishnan, and M. H. Ang. A simple rest-to-rest control command for a flexible link robot. In Proceedings of International Conference on Robotics and Automation, IEEE, Vol. 4, (1997), pp. 3312–3317.
M. Benosman, G. L. Vey, L. Lanari, and A. D. Luca. Rest-to-rest motion for planar multi-link flexible manipulator through backward recursion. Journal of Dynamic Systems, Measurement, and Control, 126, (2004), pp. 115–123. DOI: https://doi.org/10.1115/1.1649976
I. M. M. Lammerts. Adaptive computed reference computed torque control of flexible manipulators. Technische Universiteit Eindhoven, (1993).
Y. Tang, F. Sun, and Z. Sun. Neural network control of flexible-link manipulators using sliding mode. Neurocomputing, 70, (2006), pp. 288–295. DOI: https://doi.org/10.1016/j.neucom.2006.01.030
N. V. Khang and D. C. Dat. Vibration control and calculating inverse dynamics of the rigid-flexible two-link manipulator T-R. Vietnam Journal of Mechanics, 44, (2022), pp. 169–189. DOI: https://doi.org/10.15625/0866-7136/16876
J. G. de Jal ´on and E. Bayo. Kinematic and dynamic simulation of multibody systems. Springer New York, (1994).
P. B. Usoro, R. Nadira, and S. S. Mahil. A finite element/Lagrange approach to modeling lightweight flexible manipulators. Journal of Dynamic Systems, Measurement, and Control, 108, (1986), pp. 198–205. DOI: https://doi.org/10.1115/1.3143768
C. Q. Thang. Finite element method. Science and Technics Publishing House, Hanoi, (1997). (in Vietnamse).
T. I. Thinh and N. N. Khoa. Finite element method. Science and Technics Publishing House, Hanoi, (2007). (in Vietnamse).
N. V. Khang. Dynamics of multibody systems. Science and Technics Publishing House, Hanoi, (2017). (in Vietnamese).
N. V. Khang. Kronecker product and a new matrix form of Lagrangian equations with multipliers for constrained multibody systems. Mechanics Research Communications, 38, (2011), pp. 294–299. DOI: https://doi.org/10.1016/j.mechrescom.2011.04.004
J. Baumgarte. Stabilization of constraints and integrals of motion in dynamical systems. Computer Methods in Applied Mechanics and Engineering, 1, (1972), pp. 1–16. DOI: https://doi.org/10.1016/0045-7825(72)90018-7
Downloads
Published
License
This work is licensed under a Creative Commons Attribution-ShareAlike 4.0 International License.
