Effect of initial stress on the reflection and transmission of shear horizontal waves at the interface between two transversely isotropic elastic half-spaces

Do Xuan Tung

doi:10.15625/0866-7136/21949

Author affiliations

Authors

Do Xuan Tung Faculty of Civil Engineering, Hanoi Architectural University, Km 10 Nguyen Trai street, Thanh Xuan district, Hanoi, Vietnam https://orcid.org/0000-0001-6731-4109

DOI:

https://doi.org/10.15625/0866-7136/21949

Keywords:

reflection, transmission, transversely isotropic, initial stress, imperfect interface

Abstract

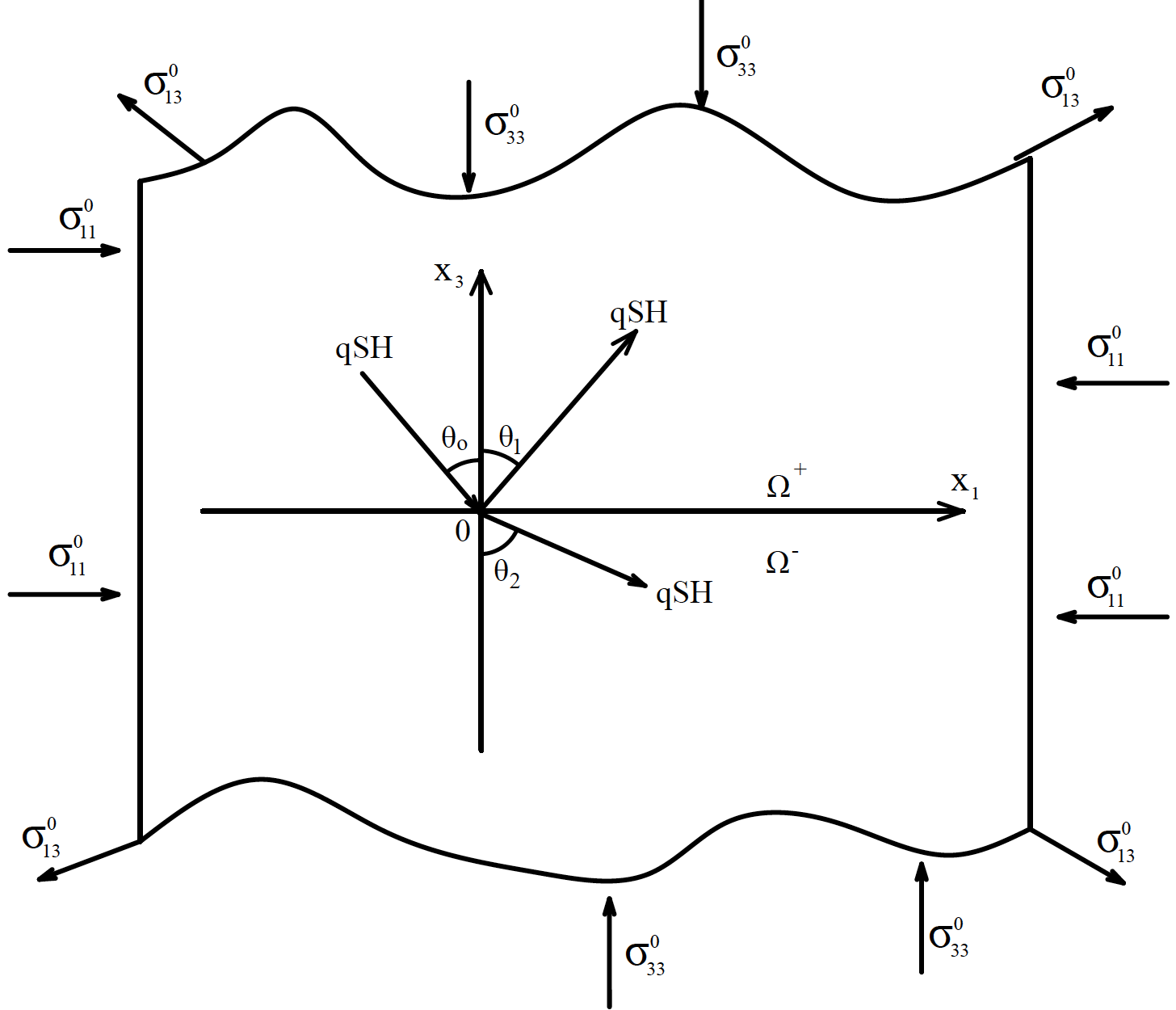
The phenomenon of reflection and transmission of shear wave (horizontally polarized) at an imperfect interface between two different transversely isotropic elastic half-spaces is investigated in this paper. First, the characteristic equation in the transversely isotropic half-space is derived. The forms of the incident, reflected, and transmitted waves are derived. Then, from the interface conditions for two cases (perfect and imperfect interfaces), the displacement and stress are required to be satisfied. The reflection and transmission coefficients in terms of the amplitude ratio of various waves are calculated using interface continuous conditions. The energy ratios of reflected and transmitted waves of the structures have been computed and shown to observe the law of conservation of energy. Numerical examples are shown graphically to exhibit the effects of initial stress as well as the imperfect interface on the phase velocity, phase angles, and reflection and transmission coefficients.

Downloads

References

[1] M. Kumari, M. Kumar, and M. S. Barak. Wave propagation characteristics at the welded interface of double-porosity solid and double-porosity dual-permeability materials. Waves in Random and Complex Media, 31, (2019), pp. 1682–1707. https://doi.org/10.1080/17455030.2019.1698789.

[2] M. A. Biot. The influence of initial stress on elastic waves. Journal of Applied Physics, 11, (1940), pp. 522–530. https://doi.org/10.1063/1.1712807.

[3] M. A. Biot. Mechanics of incremental deformations. John Wiley, New York, (1965). https://doi.org/10.1115/1.3627365.

[4] A. Chattopadhyay, S. Bose, and M. Chakraborty. Reflection of elastic waves under initial stress at a free surface: P and SV motion. The Journal of the Acoustical Society of America, 72, (1982), pp. 255–263. https://doi.org/10.1121/1.387987.

[5] N. Garg. Existence of longitudinal waves in pre-stressed anisotropic elastic medium. Journal of Earth System Science, 118, (2009), pp. 677–687. https://doi.org/10.1007/s12040-009-0053-2.

[6] S. Guha and A. Kumar Singh. Effects of initial stresses on reflection phenomenon of plane waves at the free surface of a rotating piezothermoelastic fiber-reinforced composite half-space. International Journal of Mechanical Sciences, 181, (2020). https://doi.org/10.1016/j.ijmecsci.2020.105766.

[7] H. Liu, Z. K. Wang, and T. J. Wang. Effect of initial stress on the propagation behavior of Love waves in a layered piezoelectric structure. International Journal of Solids and Structures, 38, (2001), pp. 37–51. https://doi.org/10.1016/s0020-7683(00)00009-3.

[8] K. Helbig and M. Schoenberg. Anomalous polarization of elastic waves in transversely isotropic media. The Journal of the Acoustical Society of America, 81, (1987), pp. 1235–1245. https://doi.org/10.1121/1.394527.

[9] R. Rodríguez-Ramos, H. Calás, J. A. Otero, V. Guerra, A. Ramos, and Y. S. Wang. Shear horizontal wave in multilayered piezoelectric structures: Effect of frequency, incidence angle and constructive parameters. International Journal of Solids and Structures, 48, (2011), pp. 2941– 2947. https://doi.org/10.1016/j.ijsolstr.2011.06.011.

[10] A. A. Alvarez-Mesquida, R. Rodriguez-Ramos, F. Comas, G. Monsivais, and R. Esquivel-Sirvent. Scattering of shear horizontal piezoelectric waves in piezocomposite media. Journal of Applied Physics, 89, (2001), pp. 2886–2892. https://doi.org/10.1063/1.1345517.

[11] Z. Qian, F. Jin, K. Kishimoto, and Z. Wang. Effect of initial stress on the propagation behavior of SH-waves in multilayered piezoelectric composite structures. Sensors and Actuators A: Physical, 112, (2004), pp. 368–375. https://doi.org/10.1016/j.sna.2004.02.004.

[12] Z. Hashin. The spherical inclusion with imperfect interface. Journal of Applied Mechanics, 58, (1991), pp. 444–449. https://doi.org/10.1115/1.2897205.

[13] W. Huang and S. I. Rokhlin. Interface waves along an anisotropic imperfect interface between anisotropic solids. Journal of Nondestructive Evaluation, 11, (1992), pp. 185–198. https://doi.org/10.1007/bf00566409.

[14] M. S. Barak and V. Kaliraman. Reflection and transmission of elastic waves from an imperfect boundary between micropolar elastic solid half space and fluid saturated porous solid half space. Mechanics of Advanced Materials and Structures, 26, (14), (2018), pp. 1226–1233. https://doi.org/10.1080/15376494.2018.1432795.

[15] S. Goyal, S. Sahu, and S. Mondal. Influence of imperfect bonding on the reflection and transmission of QP-wave at the interface of two functionally graded piezoelectric materials. Wave Motion, 92, (2020). https://doi.org/10.1016/j.wavemoti.2019.102431.

[16] R. Kumar, N. Sharma, and P. Ram. Interfacial imperfection on reflection and transmission of plane waves in anisotropic micropolar media. Theoretical and Applied Fracture Mechanics, 49, (2008), pp. 305–312. https://doi.org/10.1016/j.tafmec.2008.02.007.

[17] Y. Pang and J. X. Liu. Reflection and transmission of plane waves at an imperfectly bonded interface between piezoelectric and piezomagnetic media. European Journal of Mechanics - A/Solids, 30, (2011), pp. 731–740. https://doi.org/10.1016/j.euromechsol.2011.03.008.

[18] B. Singh. Wave propagation in a prestressed piezoelectric half-space. Acta Mechanica, 211, (2009), pp. 337–344. https://doi.org/10.1007/s00707-009-0234-8.

[19] D. X. Tung. The reflection and transmission of waves at an imperfect interface between two nonlocal transversely isotropic liquid-saturated porous half-spaces. Waves in Random and Complex Media, 34, (2021), pp. 2251–2267. https://doi.org/10.1080/17455030.2021.1954265.

[20] D. X. Tung. Influence of boundary conditions on the reflection and transmission of qP-wave at an interface between two nonlocal transversely isotropic elastic half-spaces. International Journal for Computational Methods in Engineering Science and Mechanics, 24, (2022), pp. 119–127. https://doi.org/10.1080/15502287.2022.2073296.

[21] M. K. Pal and A. K. Singh. Analysis of reflection and transmission phenomenon at distinct bonding interfaces in a rotating pre-stressed functionally graded piezoelectric-orthotropic structure. Applied Mathematics and Computation, 409, (2021). https://doi.org/10.1016/j.amc.2021.126398.

[22] F. Chen, Z. Zong, A. Stovas, and X. Yin. Wave reflection and transmission coefficients for layered transversely isotropic media with vertical symmetry axis under initial stress. Geophysical Journal International, 233, (2023), pp. 1580–1595. https://doi.org/10.1093/gji/ggad011.

[23] X. Guo and P. Wei. Effects of initial stress on the reflection and transmission waves at the interface between two piezoelectric half spaces. International Journal of Solids and Structures, 51, (2014), pp. 3735–3751. https://doi.org/10.1016/j.ijsolstr.2014.07.008.

[24] N. Kumari, A. Chattopadhyay, A. K. Singh, and S. A. Sahu. Magnetoelastic shear wave propagation in pre-stressed anisotropic media under gravity. Acta Geophysica, 65, (2017), pp. 189– 205. https://doi.org/10.1007/s11600-017-0016-y.

[25] Y. Huang and X. F. Li. Shear waves guided by the imperfect interface of two magnetoelectric materials. Ultrasonics, 50, (2010), pp. 750–757. https://doi.org/10.1016/j.ultras.2010.03.001.

[26] R. Kumar, N. Sharma, and P. Ram. Reflection and transmission of micropolar elastic waves at an imperfect boundary. Multidiscipline Modeling in Materials and Structures, 4, (2008), pp. 15– 36. https://doi.org/10.1163/157361108783470388.

[27] S. Singh, A. K. Singh, and S. Guha. Impact of interfacial imperfections on the reflection and transmission phenomenon of plane waves in a porous-piezoelectric model. Applied Mathematical Modelling, 100, (2021), pp. 656–675. https://doi.org/10.1016/j.apm.2021.08.022.

[28] J. D. Achenbach. Wave propagation in elastic solids, Vol. 16 of Series in Applied Mechanics. North Holland, Amsterdam, (1973). https://doi.org/10.1115/1.3423344.