Reflection and transmission of P-waves at a very rough interface between two isotropic elastic solids
Author affiliations
DOI:
https://doi.org/10.15625/0866-7136/16272Keywords:
reflection, transmission, very rough interfaces, P waves, SV wavesAbstract
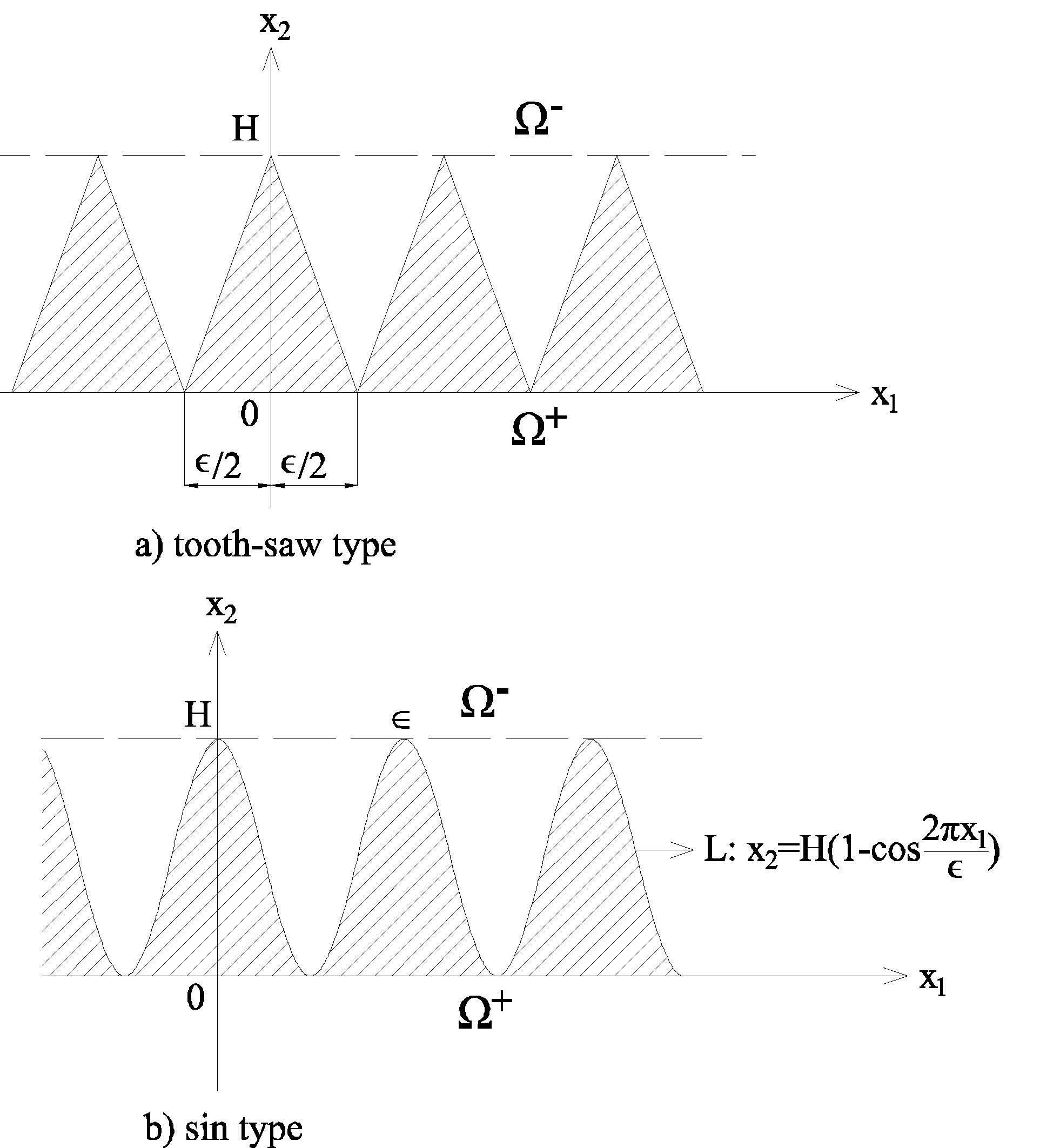
This paper deals with the reflection and transmission of P-waves at a very rough interface between two isotropic elastic solids. The interface is assumed to oscillate between two straight lines. By mean of homogenization, this problem is reduced to the reflection and transmission of P-waves through an inhomogeneous orthotropic elastic layer. It is shown that a P incident wave always creates two reflected waves (one P wave and one SV wave), however, there may exist two, one or no transmitted waves. Expressions in closed-form of the reflection and transmission coefficient have been derived using the transfer matrix of an orthotropic elastic layer. Some numerical examples are carried out to examine the reflection and transmission of P-waves at a very rough interface of tooth-comb type, tooth-saw type and sin type. It is found numerically that the reflection and transmission coefficients depend strongly on the incident angle, the incident wave frequency, the roughness and the type of interfaces.
Downloads
References
D. C. Stickler. Scattering from a soft slightly rough surface. Wave Motion, 13, (1991), pp. 211–221.
S. S. Singh and S. K. Tomar. qP-wave at a corrugated interface between two dissimilar pre-stressed elastic half-spaces. Journal of Sound and Vibration, 317, (2008), pp. 687–708.
M. van Dyke. Pertubation methods in fluid mechanics. Parabolic, Stanford, CA, (1975).
D. Talbot, J. Titchener, and J.Willis. The reflection of electromagnetic waves from very rough interfaces.Wave Motion, 12, (1990), pp. 245–260.
P. C. Vinh, D. X. Tung, and N. T. Kieu. Homogenization of very rough two-dimensional interfaces separating two dissimilar poroelastic solids with time-harmonic motions. Mathematics and Mechanics of Solids, 24, (2018), pp. 1349–1367.
A. Bensoussan, J. B. Lions, and J. Papanicolaou. Asymptotic analysis for periodic structures. North-Holland, Amsterdam, (1978).
W. Kohler, G. Papanicolaou, and S. Varadhan. Boundary and interface problems in regions with very rough boundaries. In Multiple Scattering and Waves in Random Media, North-Hollands, Amsterdam, (1981).
J. Nevard and J. B. Keller. Homogenization of rough boundaries and interfaces. SIAM Journal on Applied Mathematics, 57, (1997), pp. 1660–1686.
P. C. Vinh and D. X. Tung. Homogenized equations of the linear elasticity in two-dimensional domains with very rough interfaces. Mechanics Research Communications, 37, (2010), pp. 285–288.
P. C. Vinh and D. X. Tung. Homogenization of very rough interfaces separating two piezoelectric solids. Acta Mechanica, 224, (2013), pp. 1077–1088.
P. C. Vinh and D. X. Tung. Homogenization of rough two-dimensional interfaces separating two anisotropic solids. Journal of Applied Mechanics, 78, (2011).
J. D. Achenbach. Wave propagation in elastic solids. North-Holland, Amsterdam, (1973).
P. C. Vinh, V. T. N. Anh, and N. T. K. Linh. On a technique for deriving the explicit secular equation of Rayleigh waves in an orthotropic half-space coated by an orthotropic layer. Waves in Random and Complex Media, 26, (2016), pp. 176–188.
Downloads
Published
How to Cite
Issue
Section
License

This work is licensed under a Creative Commons Attribution-ShareAlike 4.0 International License.
Funding data
-
National Foundation for Science and Technology Development
Grant numbers 107.02-2019.314









