Analytical modeling and computational optimization for a 1-DOF compliant mechanism

Hung Dinh Nguyen, Hung Van Le, Minh Phung Dang, Hieu Giang Le, Thanh-Phong Dao
Author affiliations

Authors

  • Hung Dinh Nguyen \(^1\) Faculty of Mechanical Engineering, Industrial University of Ho Chi Minh City, Ho Chi Minh City, Vietnam
  • Hung Van Le \(^2\) Faculty of Mechanical Engineering, Ho Chi Minh City University of Technology and Education, Ho Chi Minh City, Vietnam
  • Minh Phung Dang \(^2\) Faculty of Mechanical Engineering, Ho Chi Minh City University of Technology and Education, Ho Chi Minh City, Vietnam https://orcid.org/0000-0002-8046-2410
  • Hieu Giang Le \(^2\) Faculty of Mechanical Engineering, Ho Chi Minh City University of Technology and Education, Ho Chi Minh City, Vietnam
  • Thanh-Phong Dao \(^2\) Faculty of Mechanical Engineering, Ho Chi Minh City University of Technology and Education, Ho Chi Minh City, Vietnam https://orcid.org/0000-0001-9165-4680

DOI:

https://doi.org/10.15625/0866-7136/21113

Keywords:

1-DOF compliant mechanism, equivalent stiffness, dynamic modeling, Lagrange method, finite element analysis

Abstract

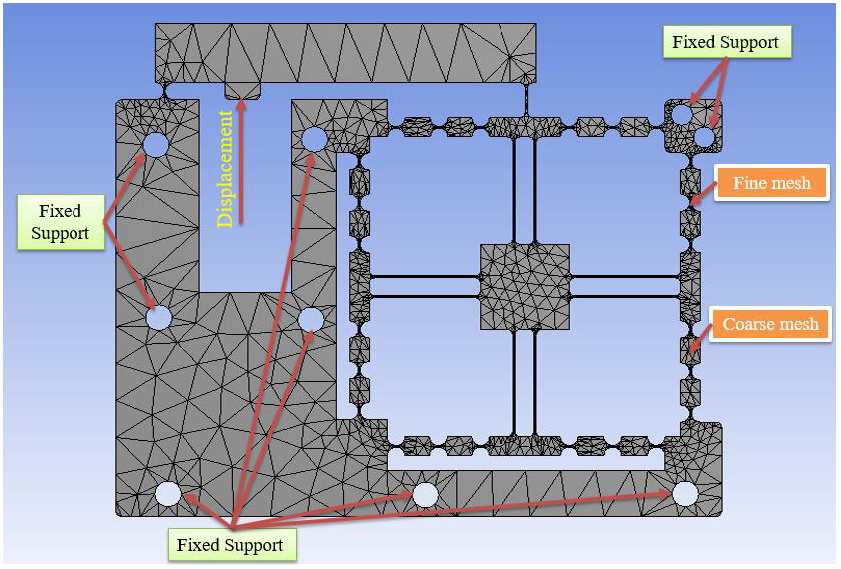
The first natural frequency directly affects the operational conditions of compliant mechanisms in precision engineering systems. To address this challenge, a computational method based on the surface response method is proposed to optimize the frequency of a new one degree of freedom (DOF) compliant mechanism. Initially, a 1-DOF 3D model of a compliant mechanism is built. The dynamic equation and the frequency response are formulated via equivalent stiffness and the Lagrange method. Subsequently, a series of numerical simulations are conducted to find the fundamental frequency of the mechanism. The initial dimensions of the flexible joints are determined, and the initial frequency is analyzed by using finite element analysis. Next, the flexible joints in the designed mechanism are optimized by a variant of the genetic algorithm. The optimized dimensions of the mechanism are found with the thickness of the circular joint of 1.10 mm, the thickness of the leaf joint of 1.19 mm, and the length of the leaf joint of 54.50 mm. The optimized result showed that there is a significant improvement in the frequency of the mechanism, increasing from an initial design of 53.218 Hz to an optimal design of 75.927 Hz with an improvement of 42.6%. This study provides important reference materials for future research on compliant mechanisms.

Downloads

Download data is not yet available.

References

[1] D. M. Ebenstein and L. A. Pruitt. Nanoindentation of biological materials. Nano Today, 1, (2006), pp. 26–33. https://doi.org/10.1016/s1748-0132(06)70077-9.

[2] N. Alderete, A. Zaheri, and H. D. Espinosa. A novel in situ experiment to investigate wear mechanisms in biomaterials. Experimental Mechanics, 59, (2019), pp. 659–667. https://doi.org/10.1007/s11340-019-00532-0.

[3] L. L. Howell, P. S. Magleby, and M. B. Olsen. Handbook of compliant mechanisms. Wiley, (2013). https://doi.org/10.1002/9781118516485.

[4] D. Stojiljković, M. Milošević, D. Ristić-Durrant, V. Nikolić, N. T. Pavlović, I. Ćirić, and N. Ivačko. Simulation, analysis, and experimentation of the compliant finger as a part of hand-compliant mechanism development. Applied Sciences, 13, (2023). https://doi.org/10.3390/app13042490.

[5] J. D. Nowak, K. A. Rzepiejewska-Malyska, R. C. Major, O. L. Warren, and J. Mich- ler. In-situ nanoindentation in the SEM. Materials Today, 12, (2010), pp. 44–45. https://doi.org/10.1016/s1369-7021(10)70144-9.

[6] Z. Hu, K. J. Lynne, S. P. Markondapatnaikuni, and F. Delfanian. Material elastic–plastic property characterization by nanoindentation testing coupled with computer modeling. Materials Science and Engineering: A, 587, (2013), pp. 268–282. https://doi.org/10.1016/j.msea.2013.08.071.

[7] L. Yuan, M. Ling, J. Lai, H. Li, and X. Zhang. Graphic transfer matrix method for kineto-static and dynamic analyses of compliant mechanisms. Journal of Mechanisms and Robotics, 16, (2023). https://doi.org/10.1115/1.4056827.

[8] N. L. Ho, M. P. Dang, and T.-P. Dao. Design and analysis of a displacement sensor-integrated compliant microgripper based on parallel structure. Vietnam Journal of Mechanics, (2020). https://doi.org/10.15625/0866-7136/14874.

[9] H. Peltola, E. Pääkkönen, P. Jetsu, and S. Heinemann. Wood based PLA and PP composites: Effect of fibre type and matrix polymer on fibre morphology, dispersion and composite properties. Composites Part A: Applied Science and Manufacturing, 61, (2014), pp. 13–22. https://doi.org/10.1016/j.compositesa.2014.02.002.

[10] N. Graupner. Application of lignin as natural adhesion promoter in cotton fibre-reinforced poly(lactic acid) (PLA) composites. Journal of Materials Science, 43, (2008), pp. 5222–5229. https://doi.org/10.1007/s10853-008-2762-3.

[11] N. L. Chau, H. G. Le, T.-P. Dao, and V. A. Dang. Design and optimization for a new compliant planar spring of upper limb assistive device using hybrid approach of RSM–FEM and MOGA. Arabian Journal for Science and Engineering, 44, (2019), pp. 7441–7456. https://doi.org/10.1007/s13369-019-03795-w.

[12] N. L. Chau, H. G. Le, V. A. Dang, and T.-P. Dao. Development and optimization for a new planar spring using finite element method, deep feedforward neural networks, and water cycle algorithm. Mathematical Problems in Engineering, 2021, (2021), pp. 1–25. https://doi.org/10.1155/2021/9921383.

[13] F. Dirksen and R. Lammering. On mechanical properties of planar flexure hinges of compliant mechanisms. Mechanical Sciences, 2, (2011), pp. 109–117. https://doi.org/10.5194/ms-2-109-2011.

[14] A. Sadollah, H. Eskandar, A. Bahreininejad, and J. H. Kim. Water cycle algorithm with evaporation rate for solving constrained and unconstrained optimization problems. Applied Soft Computing, 30, (2015), pp. 58–71. https://doi.org/10.1016/j.asoc.2015.01.050.

[15] M. Nasir, A. Sadollah, Y. H. Choi, and J. H. Kim. A comprehensive review on water cycle algorithm and its applications. Neural Computing and Applications, 32, (2020), pp. 17433–17488. https://doi.org/10.1007/s00521-020-05112-1.

[16] P. Dudek. FDM 3D printing technology in manufacturing composite elements. Archives of Metallurgy and Materials, 58, (2013), pp. 1415–1418. https://doi.org/10.2478/amm-2013-0186.

[17] V. Mazzanti, L. Malagutti, and F. Mollica. FDM 3D printing of polymers containing natural fillers: A review of their mechanical properties. Polymers, 11, (2019). https://doi.org/10.3390/polym11071094.

Downloads

Published

24-10-2024

Issue

Vol. 46 No. 4 (2024)

Section

Research Article

Categories

License

Creative Commons License

This work is licensed under a Creative Commons Attribution-ShareAlike 4.0 International License.

Crossref
Scopus
Google Scholar
Europe PMC

Funding data