Adhesive contact between two-dimensional anisotropic elastic bodies
Author affiliations
DOI:
https://doi.org/10.15625/0866-7136/19700Keywords:
adhesion, anisotropic elasticity, Stroh formalism, JKR adhesive, closed-form solutionsAbstract
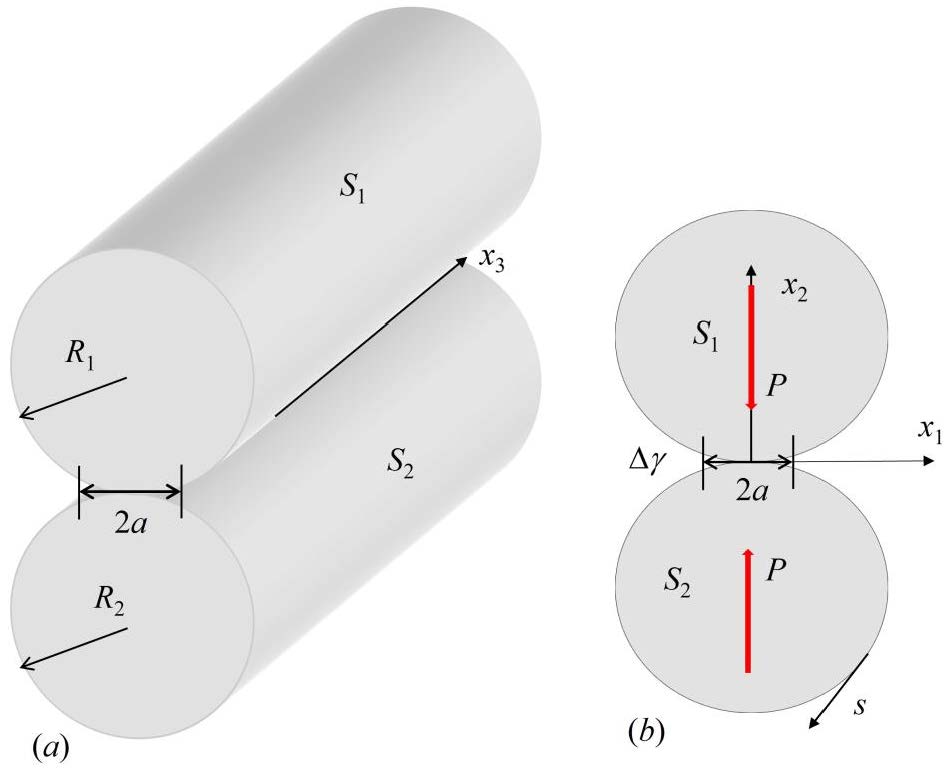
Adhesion plays a vital role in the design of smart and intelligent high-tech devices such as modern optical, microelectromechanical, and biomedical systems. However, in the literature, adhesive contact is mostly considered for contact of rigid substrates and transversely isotropic and isotropic elastic materials. The composite materials are increasingly used in the mart and intelligent high-tech devices. Since the composite materials are generally anisotropic and contact bodies are all deformable, it is more practical to consider the adhesive contact of two anisotropic elastic materials. In this paper, an adhesive contact model of anisotropic elastic bodies is established, and the closed-form solutions for two-dimensional adhesive contact of two anisotropic elastic bodies are derived. The full-field solutions and the relation for the contact region and applied force are developed using the Stroh complex variable formalism, the analytical continuation method, and concepts of the JKR adhesive model. We will show that the frictionless contact of two anisotropic elastic materials is just a special case of the present contact problem, and its solutions can be obtained by setting the work of adhesion equal to zero. In addition, we also show that our present solutions are valid for the problems of indentation by a rigid punch on an elastic half-space through a proper placement of the contact radius and the corresponding material constant. Numerical results are provided to demonstrate the accuracy, applicability, and versatility of the developed solutions.
Downloads
References
J. Zhang, G. Lin, U. Vaidya, and H. Wang. Past, present and future prospective of global carbon fibre composite developments and applications. Composites Part B: Engineering, 250, (2023).
V. M. Karbhari. Fabrication, quality and service-life issues for composites in civil engineering. In Durability of Composites for Civil Structural Applications, Elsevier, (2007), pp. 13–30.
M. Knight and D. Curliss. Composite materials. In Encyclopedia of Physical Science and Technology, Elsevier, (2003), pp. 455–468.
L. Z. Linganiso and R. D. Anandjiwala. Fibre-reinforced laminates in aerospace engineering. In Advanced Composite Materials for Aerospace Engineering, Elsevier, (2016), pp. 101–127.
F. M. Borodich. The Hertz frictional contact between nonlinear elastic anisotropic bodies (the similarity approach). International Journal of Solids and Structures, 30, (11), (1993), pp. 1513–1526.
V. T. Nguyen and C. Hwu. Indentation by multiple rigid punches on two-dimensional anisotropic elastic or viscoelastic solids. International Journal of Mechanical Sciences, 178, (2020).
V. T. Nguyen and C. Hwu. Boundary element method for two-dimensional frictional contact problems of anisotropic elastic solids. Engineering Analysis with Boundary Elements, 108, (2019), pp. 49–59.
C. Hwu and C.W. Fan. Contact problems of two dissimilar anisotropic elastic bodies. Journal of Applied Mechanics, 65, (1998), pp. 580–587.
C. Hwu and C. W. Fan. Solving the punch problems by analogy with the interface crack problems. International Journal of Solids and Structures, 35, (1998), pp. 3945–3960.
C. Hwu. Sliding punches with or without friction along the surface of an anisotropic elastic half-plane. The Quarterly Journal of Mechanics and Applied Mathematics, 51, (1998), pp. 159–177.
C. W. Fan and C. Hwu. Punch problems for an anisotropic elastic half-plane. Journal of Applied Mechanics, 63, (1996), pp. 69–76.
A. C. Fischer-Cripps. Nanoindentation. Springer New York, (2004).
S. Chen and H. Gao. Bio-inspired mechanics of reversible adhesion: Orientation-dependent adhesion strength for non-slipping adhesive contact with transversely isotropic elastic materials. Journal of the Mechanics and Physics of Solids, 55, (2007), pp. 1001–1015.
F. M. Borodich. The Hertz-type and adhesive contact problems for depth-sensing indentation. In Advances in Applied Mechanics, Elsevier, (2014), pp. 225–366.
L. Espinasse, L. Keer, F. Borodich, H. Yu, and Q. Jane Wang. A note on JKR and DMT theories of contact on a transversely isotropic half-space. Mechanics of Materials, 42, (2010), pp. 477–480.
J. R. Barber and M. Ciavarella. JKR solution for an anisotropic half space. Journal of the Mechanics and Physics of Solids, 64, (2014), pp. 367–376.
F. M. Borodich, B. A. Galanov, L. M. Keer, and M. M. Suarez-Alvarez. The JKR-type adhesive contact problems for transversely isotropic elastic solids. Mechanics of Materials, 75, (2014), pp. 34–44.
A. Delafargue and F.-J. Ulm. Explicit approximations of the indentation modulus of elastically orthotropic solids for conical indenters. International Journal of Solids and Structures, 41, (2004), pp. 7351–7360.
I. G. Goryacheva and Y. Y. Makhovskaya. Adhesive interaction of elastic bodies. Journal of Applied Mathematics and Mechanics, 65, (2001), pp. 273–282.
X. Guo and F. Jin. A generalized JKR-model for two-dimensional adhesive contact of transversely isotropic piezoelectric half-space. International Journal of Solids and Structures, 46, (2009), pp. 3607–3619.
I. Argatov. Mechanics of heterogeneous adhesive contacts. International Journal of Engineering Science, 190, (2023).
B. V. Derjaguin, V. M. Muller, and Y. P. Toporov. Effect of contact deformations on the adhesion of particles. Journal of Colloid and Interface Science, 53, (1975), pp. 314–326.
K. L. Johnson, K. Kendall, and A. D. Roberts. Surface energy and the contact of elastic solids. Proceedings of the Royal Society of London. A. Mathematical and Physical Sciences, 324, (1971), pp. 301–313.
K. L. Johnson and H. M. Pollock. The role of adhesion in the impact of elastic spheres. Journal of Adhesion Science and Technology, 8, (11), (1994), pp. 1323–1332.
C. Hwu. Anisotropic elastic plates. Springer US, (2010).
T. T. C. Ting. Anisotropic elasticity: Theory and applications. Oxford University Press, (1996).
A. N. Stroh. Dislocations and cracks in anisotropic elasticity. Philosophical Magazine, 3, (1958), pp. 625–646.
N. I. Muskhelishvili. Some basic problems of the mathematical theory of elasticity. Noordhoff Publisher, Groningen, (1954).
V. T. Nguyen and C. Hwu. A unified full field solution for indentation of an anisotropic piezoelectric half-plane by multiple rigid punches. Mechanics of Advanced Materials and Structures, 30, (2022), pp. 3897–3911.
L. Ma and A. M. Korsunsky. Interface mismatch eigenstrain of non-slipping contacts between dissimilar elastic solids. International Journal of Solids and Structures, 253, (2022).
Z. Suo. Singularities, interfaces and cracks in dissimilar anisotropic media. Proceedings of the Royal Society of London. A. Mathematical and Physical Sciences, 427, (1873), (1990), pp. 331–358.
Q.-H. Luo and Y.-T. Zhou. Adhesive behavior of transversely isotropic piezoelectric bimaterials. International Journal of Solids and Structures, 236–237, (2022).
Downloads
Published
How to Cite
Issue
Section
Categories
License

This work is licensed under a Creative Commons Attribution-ShareAlike 4.0 International License.









