An application of Rayleigh quotient for crack detection in simply supported beam
Author affiliations
DOI:
https://doi.org/10.15625/0866-7136/18182Keywords:
multiple cracked beam, Rayleigh quotient, crack identification, frequency-based methodAbstract
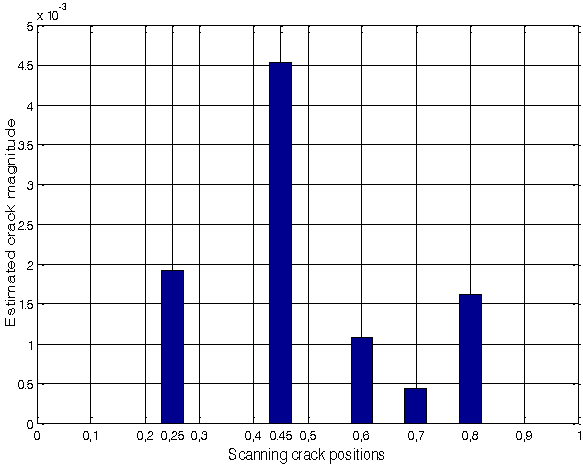
An explicit expression of natural frequencies through crack parameters is derived for multiple cracked beams with simply supported boundaries using the Rayleigh quotient. The obtained expression provides not only a simple tool for calculating natural frequencies of multiple cracked beams, but also allows employing the so-called crack scanning method for detecting multiple cracks in simply supported beams from measured natural frequencies. A numerical example demonstrates that the crack scanning method, in combination with the Rayleigh quotient, enables consistent identification of cracks with 1% relative depth.
Downloads
Metrics
References
S. W. Doebling, C. R. Farrar, M. B. Prime, and D. W. Shevitz. Damage identification and health monitoring of structural and mechanical systems from changes in their vibration characteristics: A literature review. Los Alamos National Laboratory Report, LA-13070-MS, (1996).
DOI: https://doi.org/10.2172/249299
H. Sohn, C. R. Farrar, F. M. Hemez, D. D. Shunk, D. W. Stinemates, B. R. Nadler, and J. J. Czarnecki. A review of structural health monitoring literature: 1996-2001. Los Alamos National Laboratory Report, LA-1396-MS, (2004).
W. Fan and P. Qiao. Vibration-based damage identification methods: A review and comparative study. Structural Health Monitoring, 10, (2010), pp. 83–111.
DOI: https://doi.org/10.1177/1475921710365419
Y. K. Ho and D. J. Ewins. On the structural damage identification with mode shapes. In Proceedings of the European COST F3 Conference on System Identification & Structural Health Monitoring, Universidad Politecnica de Madrid, (2000), pp. 677–684.
A. K. Pandey, M. Biswas, and M. M. Samman. Damage detection from changes in curvature mode shapes. Journal of Sound and Vibration, 145, (1991), pp. 321–332.
DOI: https://doi.org/10.1016/0022-460X(91)90595-B
C. P. Ratcliffe. Damage detection using a modified laplacian operator on mode shape data. Journal of Sound and Vibration, 204, (1997), pp. 505–517.
DOI: https://doi.org/10.1006/jsvi.1997.0961
M.-K. Yoon, D. Heider, J. W. Gillespie, C. P. Ratcliffe, and R. M. Crane. Local damage detection with the global fitting method using mode shape data in notched beams. Journal of Nondestructive Evaluation, 28, (2009), pp. 63–74.
DOI: https://doi.org/10.1007/s10921-009-0048-6
J.-B. Kim, E.-T. Lee, S. Rahmatalla, and H.-C. Eun. Non-baseline damage detection based on the deviation of displacement mode shape data. Journal of Nondestructive Evaluation, 32, (2012), pp. 14–24.
DOI: https://doi.org/10.1007/s10921-012-0154-8
P. Cawley and R. D. Adams. The location of defects in structures from measurements of natural frequencies. The Journal of Strain Analysis for Engineering Design, 14, (1979), pp. 49–57.
DOI: https://doi.org/10.1243/03093247V142049
O. S. Salawu. Detection of structural damage through changes in frequency: a review. Engineering Structures, 19, (1997), pp. 718–723.
DOI: https://doi.org/10.1016/S0141-0296(96)00149-6
N. T. Khiem and T. V. Lien. Multi-crack detection for beam by the natural frequencies. Journal of Sound and Vibration, 273, (2004), pp. 175–184.
DOI: https://doi.org/10.1016/S0022-460X(03)00424-3
G. Y. Xu,W. D. Zhu, and B. H. Emory. experimental and numerical investigation of structural damage detection using changes in natural frequencies. Journal of Vibration and Acoustics, 129, (2007), pp. 686–700.
DOI: https://doi.org/10.1115/1.2731409
Z. Xiaoqing, H. Qiang, and L. Feng. Analytical approach for detection of multiple cracks in a beam. Journal of Engineering Mechanics, 136, (2010), pp. 345–357.
DOI: https://doi.org/10.1061/(ASCE)0733-9399(2010)136:3(345)
F. B. Sayyad and B. Kumar. Identification of crack location and crack size in a simply supported beam by measurement of natural frequencies. Journal of Vibration and Control, 18, (2011), pp. 183–190.
DOI: https://doi.org/10.1177/1077546310395979
R. D. Adams, P. Cawley, C. J. Pye, and B. J. Stone. A vibration technique for non-destructively assessing the integrity of structures. Journal of Mechanical Engineering Science, 20, (1978), pp. 93–100.
DOI: https://doi.org/10.1243/JMES_JOUR_1978_020_016_02
W. M. Ostachowicz and M. Krawczuk. Analysis of the effect of cracks on the natural frequencies of a cantilever beam. Journal of Sound and Vibration, 150, (1991), pp. 191–201.
DOI: https://doi.org/10.1016/0022-460X(91)90615-Q
R. Y. Liang, J. Hu, and F. Choy. Theoretical study of crack-induced eigenfrequency changes on beam structures. Journal of Engineering Mechanics, 118, (1992), pp. 384–396.
DOI: https://doi.org/10.1061/(ASCE)0733-9399(1992)118:2(384)
Y. Narkis. Identification of crack location in vibrating simply supported beams. Journal of Sound and Vibration, 172, (1994), pp. 549–558.
DOI: https://doi.org/10.1006/jsvi.1994.1195
Q. S. Li. Vibratory characteristics of multi-step beams with an arbitrary number of cracks and concentrated masses. Applied Acoustics, 62, (2001), pp. 691–706.
DOI: https://doi.org/10.1016/S0003-682X(00)00066-9
S. Caddemi and I. Cali` o. Exact closed-form solution for the vibration modes of the Euler–Bernoulli beam with multiple open cracks. Journal of Sound and Vibration, 327, (2009), pp. 473–489.
DOI: https://doi.org/10.1016/j.jsv.2009.07.008
K. Aydin. Vibratory characteristics of euler-bernoulli beams with an arbitrary number of cracks subjected to axial load. Journal of Vibration and Control, 14, (2008), pp. 485–510.
DOI: https://doi.org/10.1177/1077546307080028
N. T. Khiem and H. T. Tran. A procedure for multiple crack identification in beam-like structures from natural vibration mode. Journal of Vibration and Control, 20, (9), (2014), pp. 1417–1427.
DOI: https://doi.org/10.1177/1077546312470478
A. Morassi. Crack-induced changes in eigenparameters of beam structures. Journal of Engineering Mechanics, 119, (1993), pp. 1798–1803.
DOI: https://doi.org/10.1061/(ASCE)0733-9399(1993)119:9(1798)
A. Morassi and M. Rollo. Identification of two cracks in a simply supported beam from minimal frequency measurements. Journal of Vibration and Control, 7, (2001), pp. 729–739.
DOI: https://doi.org/10.1177/107754630100700507
L. Rubio. An efficient method for crack identification in simply supported Euler–Bernoulli beams. Journal of Vibration and Acoustics, 131, (2009).
DOI: https://doi.org/10.1115/1.3142876
J. Lee. Identification of multiple cracks in a beam using natural frequencies. Journal of Sound and Vibration, 320, (2009), pp. 482–490.
DOI: https://doi.org/10.1016/j.jsv.2008.10.033
R. Y. Liang, J. Hu, and F. Choy. Quantitative NDE technique for assessing damages in beam structures. Journal of Engineering Mechanics, 118, (1992), pp. 1468–1487.
DOI: https://doi.org/10.1061/(ASCE)0733-9399(1992)118:7(1468)
D. P. Patil and S. K. Maiti. Detection of multiple cracks using frequency measurements. Engineering Fracture Mechanics, 70, (2003), pp. 1553–1572.
DOI: https://doi.org/10.1016/S0013-7944(02)00121-2
M.-H. H. Shen and C. Pierre. Natural modes of Bernoulli-Euler beams with symmetric cracks. Journal of Sound and Vibration, 138, (1990), pp. 115–134.
DOI: https://doi.org/10.1016/0022-460X(90)90707-7
J. Fernandez-Saez, L. Rubio, and C. Navarro. Approximate calculation of the fundamental frequency for bending vibrations of cracked beam. Journal of Sound and Vibration, 225, (1999), pp. 345–352.
DOI: https://doi.org/10.1006/jsvi.1999.2251
T. Zheng and T. Ji. An approximate method for determining the static deflection and natural frequency of a cracked beam. Journal of Sound and Vibration, 331, (2012), pp. 2654–2670.
DOI: https://doi.org/10.1016/j.jsv.2012.01.021
I. A. Karnovsky and O. I. Lebed. Formulas for structural dynamics: tables, graphs and solutions. McGraw-Hill Education, (2001).
Downloads
Published
How to Cite
License
This work is licensed under a Creative Commons Attribution-ShareAlike 4.0 International License.
Funding data
-
National Foundation for Science and Technology Development
Grant numbers 107.01-2018.304
