Vibration of electrically actuated MEMS Timoshenko microbeams based on a hierarchical beam element
Author affiliations
DOI:
https://doi.org/10.15625/0866-7136/17909Keywords:
Timoshenko microbeam, MCST, electrostatic actuation, hierarchical interpolation, nonlinear finite element analysisAbstract
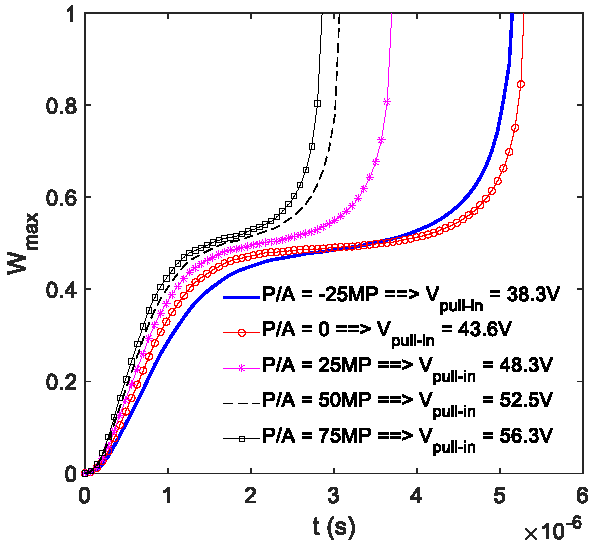
In this paper, vibration of Timoshenko microbeams with an axial force in micro-electromechanical systems (MEMS) is studied for the first time by using a nonlinear finite element procedure. Based on the von Kármán geometric nonlinearity and the modified couple stress theory (MCST), a beam element is formulated by employing hierarchical functions to interpolate the displacement field. Using the derived element, the discretized equation of motion for the microbeam is constructed and then solved by the Newton-Raphson iterative procedure in conjunction with the Newmark method. The natural frequencies, pull-in voltages and dynamic deflections are computed for a clamped-clamped microbeam under electrostatic actuation of a given direct current (DC) voltage. The numerical result reveals that the axial force and the microsize effect have a significant influence on the vibration, and the fundamental frequency of the microbeams is underestimated by ignoring the size effect. The effects of the axial force, the applied voltage and the material length scale parameter on the vibration of the beam are studied in detail and highlighted.
Downloads
Metrics
References
J. Y. Park, G. H. Kim, K. W. Chung, and J. U. Bu. Monolithically integrated micromachined RF MEMS capacitive switches. Sensors and Actuators A: Physical, 89, (2001), pp. 88–94.
DOI: https://doi.org/10.1016/S0924-4247(00)00549-5
R. K. Gupta. Electrostatic pull-in test structure design for in-situ mechanical property measurements of microelectromechanical systems (MEMS). PhD thesis, Massachusetts Institute of Technology, (1997).
B. Choi and E. G. Lovell. Improved analysis of microbeams under mechanical and electrostatic loads. Journal of Micromechanics and Microengineering, 7, (1997), pp. 24–29.
DOI: https://doi.org/10.1088/0960-1317/7/1/005
E. M. Abdel-Rahman, M. I. Younis, and A. H. Nayfeh. Characterization of the mechanical behavior of an electrically actuated microbeam. Journal of Micromechanics and Microengineering, 12, (2002), pp. 759–766.
DOI: https://doi.org/10.1088/0960-1317/12/6/306
M. I. Younis, E. M. Abdel-Rahman, and A. Nayfeh. A reduced-order model for electrically actuated microbeam-based MEMS. Journal of Microelectromechanical Systems, 12, (2003), pp. 672–680.
DOI: https://doi.org/10.1109/JMEMS.2003.818069
M. I. Younis and A. H. Nayfeh. A study of the nonlinear response of a resonant microbeam to an electric actuatio. Nonlinear Dynamics, 31, (1), (2003), pp. 91–117.
DOI: https://doi.org/10.1023/A:1022103118330
E. M. Abdel-Rahman and A. H. Nayfeh. Secondary resonances of electrically actuated resonant microsensors. Journal of Micromechanics and Microengineering, 13, (2003), pp. 491–501.
DOI: https://doi.org/10.1088/0960-1317/13/3/320
S. Chaterjee and G. Pohit. A large deflection model for the pull-in analysis of electrostatically actuated microcantilever beams. Journal of Sound and Vibration, 322, (2009), pp. 969–986.
DOI: https://doi.org/10.1016/j.jsv.2008.11.046
M. I. Younis. MEMS linear and nonlinear statics and dynamics. Springer US, (2011).
DOI: https://doi.org/10.1007/978-1-4419-6020-7
G. Rezazadeh, H. Sadeghian, I. Hosseinzadeh, and A. Toloei. Investigation of pull-in phenomenon on extensible micro beam subjected to electrostatic pressure. Sensors & Transducers Journal, 79, (5), (2007), pp. 1173–1179.
M. R. Ghazavi, G. Rezazadeh, and S. Azizi. Finite element analysis of static and dynamic pull-in instability of a fixed-fixed micro beam considering damping effects. Sensors & Transducers, 103, (4), (2009), p. 132.
A. J. Kaneria, D. S. Sharma, and R. R. Trivedi. Static analysis of electrostatically actuated micro cantilever beam. Procedia Engineering, 51, (2013), pp. 776–780.
DOI: https://doi.org/10.1016/j.proeng.2013.01.111
J.-H. Kuang and C.-J. Chen. The nonlinear electrostatic behavior for shaped electrode actuators. International Journal of Mechanical Sciences, 47, (2005), pp. 1172–1190.
DOI: https://doi.org/10.1016/j.ijmecsci.2005.04.006
D. C. C. Lam, F. Yang, A. C. M. Chong, J. Wang, and P. Tong. Experiments and theory in strain gradient elasticity. Journal of the Mechanics and Physics of Solids, 51, (2003), pp. 1477–1508.
DOI: https://doi.org/10.1016/S0022-5096(03)00053-X
M. H. Kahrobaiyan, M. Asghari, M. Rahaeifard, and M. T. Ahmadian. A nonlinear strain gradient beam formulation. International Journal of Engineering Science, 49, (2011), pp. 1256–1267.
DOI: https://doi.org/10.1016/j.ijengsci.2011.01.006
F. Yang, A. C. M. Chong, D. C. C. Lam, and P. Tong. Couple stress based strain gradient theory for elasticity. International Journal of Solids and Structures, 39, (2002), pp. 2731–2743.
DOI: https://doi.org/10.1016/S0020-7683(02)00152-X
H. Farokhi and M. H. Ghayesh. Size-dependent behaviour of electrically actuated microcantilever-based MEMS. International Journal of Mechanics and Materials in Design, 12, (2015), pp. 301–315.
DOI: https://doi.org/10.1007/s10999-015-9295-0
M. H. Ghayesh and H. Farokhi. Nonlinear behaviour of electrically actuated microplatebased MEMS resonators. Mechanical Systems and Signal Processing, 109, (2018), pp. 220–234.
DOI: https://doi.org/10.1016/j.ymssp.2017.11.043
M. Baghani. Analytical study on size-dependent static pull-in voltage of microcantilevers using the modified couple stress theory. International Journal of Engineering Science, 54, (2012), pp. 99–105.
DOI: https://doi.org/10.1016/j.ijengsci.2012.01.001
M. H. Ghayesh, H. Farokhi, and M. Amabili. Nonlinear behaviour of electrically actuated MEMS resonators. International Journal of Engineering Science, 71, (2013), pp. 137–155.
DOI: https://doi.org/10.1016/j.ijengsci.2013.05.006
Y. C. Hu, C. M. Chang, and S. C. Huang. Some design considerations on the electrostatically actuated microstructures. Sensors and Actuators A: Physical, 112, (2004), pp. 155–161.
DOI: https://doi.org/10.1016/j.sna.2003.12.012
P. M. Osterberg and S. D. Senturia. M-TEST: A test chip for MEMS material property measurement using electrostatically actuated test structures. Journal of Microelectromechanical Systems, 6, (1997), pp. 107–118.
DOI: https://doi.org/10.1109/84.585788
C. I. Le, Q. D. Tran, V. D. Lam, and D. K. Nguyen. Size-dependent behavior of a MEMS microbeam under electrostatic actuation. Vietnam Journal of Mechanics, 44, (2022), pp. 69–81.
DOI: https://doi.org/10.15625/0866-7136/16834
R. P. Shimpi and H. G. Patel. Free vibrations of plate using two variable refined plate theory. Journal of Sound and Vibration, 296, (2006), pp. 979–999.
DOI: https://doi.org/10.1016/j.jsv.2006.03.030
R. D. Cook. Concepts and applications of finite element analysis. JohnWiley & Sons, (2007).
D. K. Nguyen and V. T. Bui. Dynamic analysis of functionally graded Timoshenko beams in thermal environment using a higher-order hierarchical beam element. Mathematical Problems in Engineering, 2017, (2017), pp. 1–12.
DOI: https://doi.org/10.1155/2017/7025750
J. E. Akin. Finite elements for analysis and design: computational mathematics and applications series. Elsevier, (2014).
A. Tessler and S. B. Dong. On a hierarchy of conforming timoshenko beam elements. Computers & Structures, 14, (1981), pp. 335–344.
DOI: https://doi.org/10.1016/0045-7949(81)90017-1
A. Ghali, A. M. Neville, and T. G. Brown. Structural analysis: A unified classical and matrix approach. CRC Press, 6th edition, (2017).
DOI: https://doi.org/10.1201/9781315273006
Downloads
Published
How to Cite
License
This work is licensed under a Creative Commons Attribution-ShareAlike 4.0 International License.
