Size-dependent behavior of a MEMS microbeam under electrostatic actuation
Author affiliations
DOI:
https://doi.org/10.15625/0866-7136/16834Keywords:
microbeam, modified couple stress theory, electrostatic actuation, refined third-order shear deformation theory, nonlinear finite element analysisAbstract
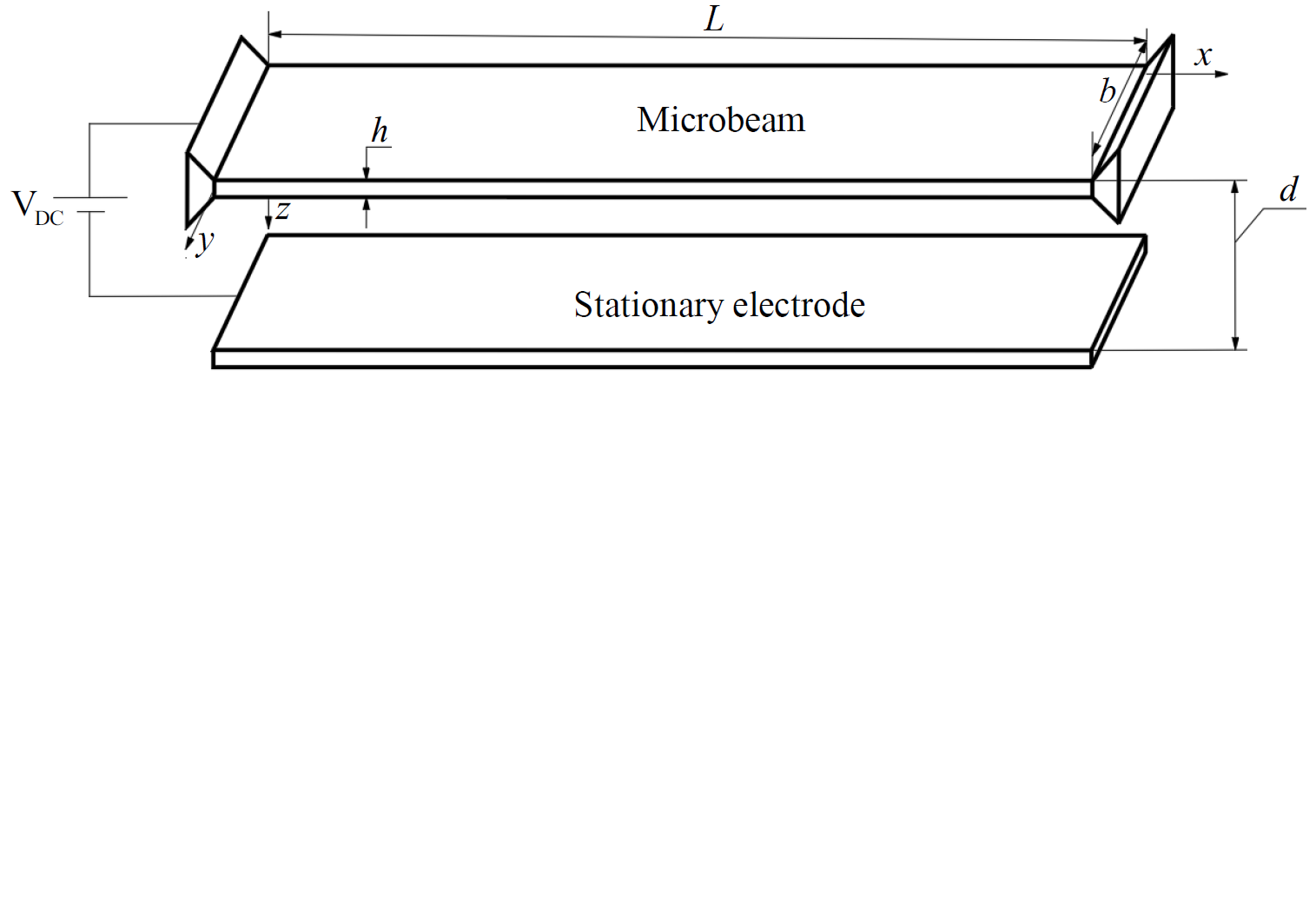
The size-dependent behavior of a silicon microbeam with an axial force in MEMS is studied using a nonlinear finite element procedure. Based on a refined third-order shear deformation theory and the modified couple stress theory (MCST), nonlinear differential equations of motion for the beam are derived from Hamilton’s principle, and they are transferred to a discretized form using a two-node beam element. Newton-Raphson based iterative procedure is used in conjunction with Newmark method to obtain the pull-in voltages and deflections of a clamped-clamped microbeam under electrostatic actuation. The influence of the axial force, applied voltage and material length scale parameter on the behavior of the beam is studied in detail and highlighted.
Downloads
References
B. Choi and E. G. Lovell. Improved analysis of microbeams under mechanical and electrostatic loads. Journal of Micromechanics and Microengineering, 7, (1), (1997).
E. Abdel-Rahman, M. Younis, and A. Nayfeh. Characterization of the mechanical behavior of an electrically actuated microbeam. Journal of Micromechanics and Microengineering, 12, (6), (2002).
M. I. Younis, E. M. Abdel-Rahman, and A. Nayfeh. A reduced-order model for electrically actuated microbeam-based MEMS. Journal of Microelectromechanical Systems, 12, (5), (2003),
M. I. Younis and A. H. Nayfeh. A study of the nonlinear response of a resonant microbeam to an electric actuation. Nonlinear Dynamics, 31, (1), (2003), pp. 91–117.
E. M. Abdel-Rahman and A. H. Nayfeh. Secondary resonances of electrically actuated resonant microsensors. Journal of Micromechanics and Microengineering, 13, (3), (2003).
S. Chaterjee and G. Pohit. A large deflection model for the pull-in analysis of electrostatically actuated microcantilever beams. Journal of Sound and Vibration, 322, (4-5), (2009), pp. 969–986.
M. R. Ghazavi, G. Rezazadeh, and S. Azizi. Finite element analysis of static and dynamic pull-in instability of a fixed-fixed micro beam considering damping effects. Sensors & Transducers, 103, (4), (2009).
G. Rezazadeh, H. Sadeghian, I. Hosseinzadeh, and A. Toloei. Investigation of pull-in phenomenon on extensible micro beam subjected to electrostatic pressure. Sensors & Transducers Journal, 79, (5), (2007), pp. 1173–1179.
A. J. Kaneria, D. S. Sharma, and R. R. Trivedi. Static analysis of electrostatically–actuated micro cantilever beam. Procedia Engineering, 51, (2013), pp. 776–780.
H. Farokhi and M. H. Ghayesh. Size-dependent behaviour of electrically actuated microcantilever-based MEMS. International Journal of Mechanics and Materials in Design, 12, (3), (2016), pp. 301–315.
M. H. Ghayesh and H. Farokhi. Nonlinear behaviour of electrically actuated microplatebased MEMS resonators. Mechanical Systems and Signal Processing, 109, (2018), pp. 220–234.
M. Baghani. Analytical study on size-dependent static pull-in voltage of microcantilevers using the modified couple stress theory. International Journal of Engineering Science, 54, (2012), pp. 99–105.
M. H. Ghayesh, H. Farokhi, and M. Amabili. Nonlinear behaviour of electrically actuated MEMS resonators. International Journal of Engineering Science, 71, (2013), pp. 137–155.
R. P. Shimpi and H. G. Patel. Free vibrations of plate using two variable refined plate theory. Journal of Sound and Vibration, 296, (4-5), (2006), pp. 979–999.
F. A. C. M. Yang, A. C. M. Chong, D. C. C. Lam, and P. Tong. Couple stress based strain gradient theory for elasticity. International Journal of Solids and Structures, 39, (10), (2002), pp. 2731–2743.
Y.-C. Hu, C. M. Chang, and S. C. Huang. Some design considerations on the electrostatically actuated microstructures. Sensors and Actuators A: Physical, 112, (1), (2004), pp. 155–161.
C. I. Le, N. A. T. Le, and D. K. Nguyen. Free vibration and buckling of bidirectional functionally graded sandwich beams using an enriched third-order shear deformation beam element. Composite Structures, 261, (2021).
R. D. Cook. Concepts and applications of finite element analysis. JohnWiley & Sons, (2002).
P. M. Osterberg and S. D. Senturia. M-TEST: a test chip for MEMS material property measurement using electrostatically actuated test structures. Journal of Microelectromechanical systems, 6, (2), (1997), pp. 107–118.
M. I. Younis. MEMS linear and nonlinear statics and dynamics. Springer Science & Business Media, Vol. 20, (2011).
Downloads
Published
How to Cite
Issue
Section
License

This work is licensed under a Creative Commons Attribution-ShareAlike 4.0 International License.









