Nonlocal effects on Rayleigh-type surface wave in a micropolar piezoelectric medium
Author affiliations
DOI:
https://doi.org/10.15625/0866-7136/16539Keywords:
nonlocality, microrotation, piezoelectricity, Rayleigh wave, dispersionAbstract
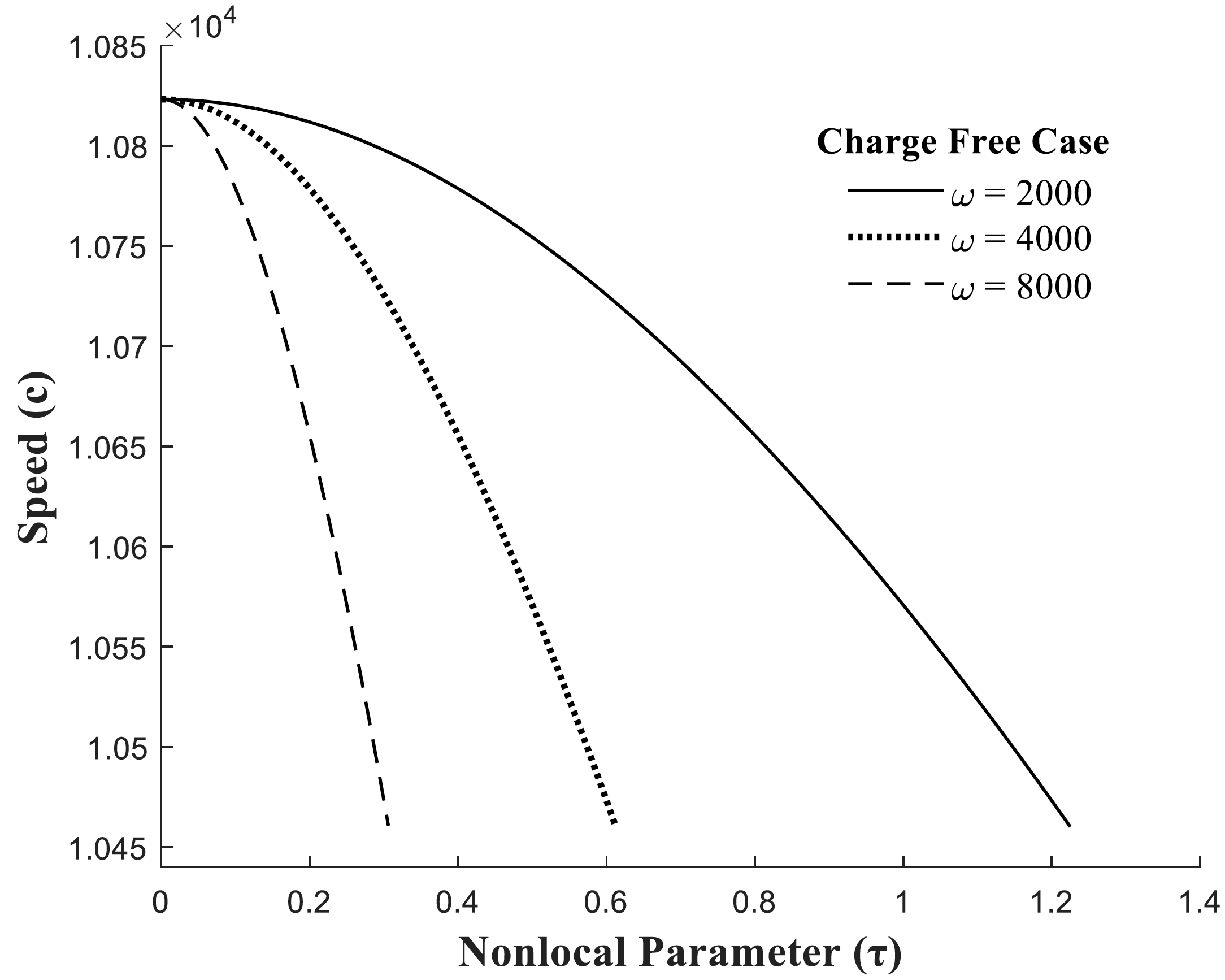
The properties of Rayleigh-type surface wave in a linear, homogeneous and transversely isotropic nonlocal micropolar piezoelectric solid half-space are explored. Dispersion relations for Rayleigh-type surface wave are derived for both charge free and electrically shorted cases. Using an algorithm of iteration method in MATLAB software, the wave speed of Rayleigh wave is computed for relevant material constants. The effects of nonlocality, angular frequency, micropolarity and piezoelectricity are illustrated graphically on the propagation speed of Rayleigh wave.
Downloads
References
L. Rayleigh. On waves propagated along the plane surface of an elastic solid. Proceedings of the London Mathematical Society, s1-17, (1885), pp. 4–11.
V. A. Sveklo. Plane waves and Rayleigh waves in anisotropic media. Dokl. Akad. Nauk SSSR, 59, (1948), pp. 871–874.
L. Gold. Rayleigh wave propagation on anisotropic (cubic) media. Physical Review, 104, (1956), pp. 1532–1536.
W.W. Johnson. The propagation of Stoneley and Rayleigh waves in anisotropic elastic media. Bulletin of the Seismological Society of America, 60, (4), (1970), pp. 1105–1122.
D. Royer and E. Dieulesaint. Rayleigh wave velocity and displacement in orthorhombic, tetragonal, hexagonal, and cubic crystals. The Journal of the Acoustical Society of America, 76, (1984), pp. 1438–1444.
M. Destrade. Rayleigh waves in anisotropic crystals rotating about the normal to a symmetry plane. Journal of Applied Mechanics, 71, (2004), pp. 516–520.
P. C. Vinh and R. W. Ogden. On the Rayleigh wave speed in orthotropic elastic solids. Meccanica, 40, (2005), pp. 147–161.
A. Rehman, A. Khan, and A. Ali. Rotational effects on Rayleigh wave speed in orthotropic medium. Punjab University Journal of Mathematics, 39, (2007), pp. 29–33,
A. M. Abd-Alla, S. M. Abo-Dahab, and T. A. Al-Thamali. Propagation of Rayleigh waves in a rotating orthotropic material elastic half-space under initial stress and gravity. Journal of Mechanical Science and Technology, 26, (9), (2012), pp. 2815–2823.
G. Sudheer, M. H. Lakshmi, and Y. V. Rao. A note on formulas for the Rayleigh wave speed in elastic solids. Ultrasonics, 73, (2017), pp. 82–87.
S. Kundu, M. Maity, D. K. Pandit, and S. Gupta. Effect of initial stress on the propagation and attenuation characteristics of Rayleigh waves. Acta Mechanica, 230, (2018), pp. 67–85.
B. Singh and B. Kaur. Rayleigh-type surface wave on a rotating orthotropic elastic half-space with impedance boundary conditions. Journal of Vibration and Control, 26, (2020), pp. 1980–1987.
B. Singh and B. Kaur. Rayleigh surface wave at an impedance boundary of an incompressible micropolar solid half-space. Mechanics of Advanced Materials and Structures, (2021), pp. 1–12.
B. Kaur and B. Singh. Rayleigh waves on the impedance boundary of a rotating monoclinic half-space. Acta Mechanica, 232, (2021), pp. 2479–2491.
A. C. Eringen. Theory of nonlocal elasticity and some applications. Res Mechanica, (1987), pp. 313–342.
D. G. B. Edelen and N. Laws. On the thermodynamics of systems with nonlocality. Archive for Rational Mechanics and Analysis, 43, (1971), pp. 24–35.
D. G. B. Edelen, A. E. Green, and N. Laws. Nonlocal continuum mechanics. Archive for Rational Mechanics and Analysis, 43, (1971), pp. 36–44.
A. C. Eringen. Nonlocal polar elastic continua. International Journal of Engineering Science, 10, (1972), pp. 1–16.
A. C. Eringen. Linear theory of nonlocal elasticity and dispersion of plane waves. International Journal of Engineering Science, 10, (1972), pp. 425–435.
A. C. Eringen and D. G. B. Edelen. On nonlocal elasticity. International Journal of Engineering Science, 10, (1972), pp. 233–248.
A. C. Eringen. Linear theory of nonlocal microelasticity and dispersion of plane waves. Lett. Appl. Eng. Sci., 1, (1973), pp. 129–146.
S. Chirita. Nonlocal effects on the stress distribution in an elastic half space. Accad. Naz. Lincei, serie viii, LX fasc., 6, (1976), pp. 802–807.
D. Ieşan. Reciprocal theorems and variational theorems in nonlocal elastodynamics. International Journal of Engineering Science, 15, (1977), pp. 693–699.
A. C. Eringen. Plane waves in nonlocal micropolar elasticity. International Journal of Engineering Science, 22, (1984), pp. 1113–1121.
B. S. Altan. Uniqueness in linear theory of nonlocal elasticity. Bulletin of the Technical University of Istanbul, (1984).
W. Jun and R. S. Dhaliwal. On some theorems in the nonlocal theory of micropolar elasticity. International Journal of Solids and Structures, 30, (10), (1993), pp. 1331–1338.
A. C. Eringen. Nonlocal continuum field theories. Springer Verlag, New York, (2001).
A. Khurana and S. K. Tomar. Reflection of plane longitudinal waves from the stress-free boundary of a nonlocal, micropolar solid half-space. Journal of Mechanics of Materials and Structures, 8, (2013), pp. 95–107.
A. Khurana and S. K. Tomar.Wave propagation in nonlocal microstretch solid. Applied Mathematical Modelling, 40, (2016), pp. 5858–5875.
A. Khurana and S. K. Tomar. Rayleigh-type waves in nonlocal micropolar solid half-space. Ultrasonics, 73, (2017), pp. 162–168.
A. Khurana and S. K. Tomar. Waves at interface of dissimilar nonlocal micropolar elastic half-spaces. Mechanics of Advanced Materials and Structures, 26, (2018), pp. 825–833.
I. Roy, D. P. Acharya, and S. Acharya. Rayleigh wave in a rotating nonlocal magnetoelastic half-plane. Journal of Theoretical and Applied Mechanics, 45, (2015), pp. 61–78.
G. Kaur, D. Singh, and S. K. Tomar. Rayleigh-type wave in a nonlocal elastic solid with voids. European Journal of Mechanics - A/Solids, 71, (2018), pp. 134–150.
G. Kaur, D. Singh, and S. K. Tomar. Love waves in a nonlocal elastic media with voids. Journal of Vibration and Control, 25, (2019), pp. 1470–1483. h
D. X. Tung. Dispersion equation of Rayleigh waves in transversely isotropic nonlocal piezoelastic solids half-space. Vietnam Journal of Mechanics, 41, (2019), pp. 363–371.
B. Singh. Rayleigh-type surface waves in a nonlocal thermoelastic solid half space with voids. Waves in Random and Complex Media, 31, (2020), pp. 2103–2114.
S. Biswas. Surface waves in porous nonlocal thermoelastic orthotropic medium. Acta Mechanica, 231, (2020), pp. 2741–2760.
B. Kaur and B. Singh. Rayleigh-type surface wave in nonlocal isotropic diffusive materials. Acta Mechanica, 232, (2021), pp. 3407–3416.
D. X. Tung. The reflection and transmission of a quasi-longitudinal displacement wave at an imperfect interface between two nonlocal orthotropic micropolar half-spaces. Archive of Applied Mechanics, 91, (2021), pp. 4313–4328.
A. C. Eringen. Linear theory of micropolar elasticity. Journal of Mathematics and Mechanics, 15, (1966), pp. 909–923.
A. C. Eringen. Theory of micropolar elasticity in Fracture, Vol. 2. Academic Press, (1968).
A. C. Eringen. Microcontinuum field theories I: Foundations and soilds. Springer, New York, (1999).
I. A. Crǎciun. Uniqueness theorem in the linear theory of piezoelectric micropolar thermoelasticity ion. International Journal of Engineering Science, 33, (1995), pp. 1027–1036.
S. G. Ciumasu and D. Vieru. Variational formulations for the vibration of a micropolar piezoelectric body. The Journal of the Acoustical Society of America, 105, (1999), pp. 1240–1240.
D. Vieru and S. G. Ciumasu. Love waves in nonclassical micropolar piezoelectricity. The Journal of the Acoustical Society of America, 105, (1999), pp. 1241–1241.
P. A. Zhilin and Y. E. Kolpakov. A micro-polar theory for piezoelectric materials in Proceedings of the Advanced Problems in Mechanics. Lecture at XXXIII Summer School-Conference, St, Petersburg, Russia, (2005).
M. Aouadi. Aspects of uniqueness in micropolar piezoelectric bodies. Mathematics and Mechanics of Solids, 13, (2008), pp. 499–512.
C. Galeş. Some results in micromorphic piezoelectricity. European Journal of Mechanics - A/Solids, 31, (2012), pp. 37–46.
B. Singh and R. Sindhu. On propagation of Rayleigh type surface wave in a micropolar piezoelectric medium. Open Journal of Acoustics, 06, (04), (2016), pp. 35–44.
B. Singh and R. Sindhu. Rotational effects on propagation of Rayleigh wave in a micropolar piezoelectric medium. Journal of Theoretical and Applied Mechanics, 48, (2018), pp. 93–105.
A. Sangwan, B. Singh, and J. Singh. Reflection and transmission of plane waves ast an interface between elastic and micropolar piezoelectric solid half-spaces. Technische Mechanik, 38, (3), (2018), pp. 267–285.
B. Singh, A. Sangwan, and J. Singh. Reflection and transmission of elastic waves at an interface between two micropolar piezoelectric half-spaces. Journal of Ocean Engineering and Science, 4, (2019), pp. 227–237.
R. Bijarnia, B. Singh, and J. Awrejcewicz. Reflection at non-free boundary of a micropolar piezoelectric half-space. Forces in Mechanics, 3, (2021).
A. C. Eringen. On differential equations of nonlocal elasticity and solutions of screw dislocation and surface waves. Journal of Applied Physics, 54, (1983), pp. 4703–4710.
Downloads
Published
How to Cite
Issue
Section
License

This work is licensed under a Creative Commons Attribution-ShareAlike 4.0 International License.









