Frequency response sensitivity to crack for piezoelectric FGM beam subjected to moving load
Author affiliations
DOI:
https://doi.org/10.15625/0866-7136/20933Keywords:
FGM beam, piezoelectric layer, frequency response, moving load, sensitivity analysisAbstract
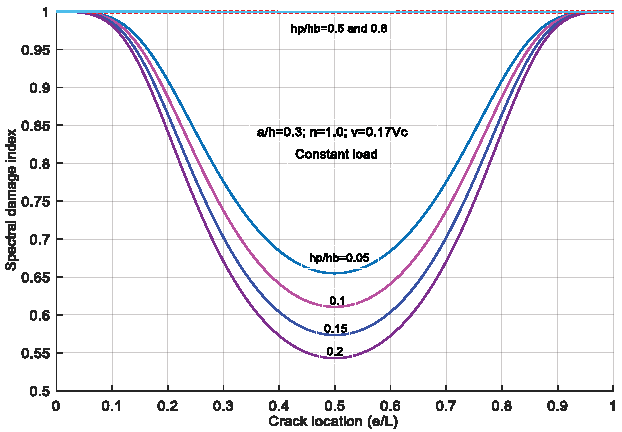
Since functionally graded material (FGM) is increasingly used in high-tech engineering, free and forced vibrations of FGM structures become an important issue. This report addresses the analysis of frequency response sensitivity to crack for piezoelectric FGM beams subjected to moving load. First, a frequency domain model of a cracked FGM beam with a piezoelectric layer is conducted to derive an explicit expression of the electrical charge produced in the piezoelectric layer under the moving load. It was shown in the previous works of the authors that the electrical charge is a reliable representation of the beam frequency response to moving load and can be efficiently employed as a measured diagnostic signal for structural health monitoring. Then, a damage indicator acknowledged as a spectral damage index (SDI) calculated from the electrical frequency response is introduced and used for sensitivity analysis of the response to crack. Under the sensitivity analysis the effect also of FGM and moving load parameters on the sensitivity is examined and illustrated by numerical results.
Downloads
References
[1] H. Sohn, C. R. Farrar, F. M. Hemez, and J. J. Czarnecki. A review of structural health review of structural health monitoring literature 1996-2001. Los Alamos National Laboratory Report, (2002).
[2] W. Fan and P. Qiao. Vibration-based damage identification methods: A review and comparative study. Structural Health Monitoring, 10, (2010), pp. 83–111. https://doi.org/10.1177/1475921710365419.
[3] R. Hou and Y. Xia. Review on the new development of vibration-based damage identification for civil engineering structures: 2010–2019. Journal of Sound and Vibration, 491, (2021). https://doi.org/10.1016/j.jsv.2020.115741.
[4] S. S. Rao and M. Sunar. Piezoelectricity and its use in disturbance sensing and control of flexible structures: A survey. Applied Mechanics Reviews, 47, (1994), pp. 113–123. https://doi.org/10.1115/1.3111074.
[5] G. Park, H. Sohn, C. R. Farrar, and D. J. Inman. Overview of piezoelectric impedance-based health monitoring and path forward. The Shock and Vibration Digest, 35, (2003), pp. 451–463. https://doi.org/10.1177/05831024030356001.
[6] V. Giurgiutiu. Structural health monitoring with piezoelectric wafer active sensors. Academic Press, Oxford, (2007).
[7] W. H. Duan, Q. Wang, and S. T. Quek. Applications of piezoelectric materials in structural health monitoring and repair: Selected research examples. Materials, 3, (2010), pp. 5169–5194. https://doi.org/10.3390/ma3125169.
[8] H. S. Tzou and C. I. Tseng. Distributed piezoelectric sensor/actuator design for dynamic measurement/control of distributed parameter systems: A piezoelectric finite element approach. Journal of Sound and Vibration, 138, (1990), pp. 17–34. https://doi.org/10.1016/0022-460x(90)90701-z.
[9] E. F. Crawley and J. de Luis. Use of piezoelectric actuators as elements of intelligent structures. AIAA Journal, 25, (1987), pp. 1373–1385. https://doi.org/10.2514/3.9792.
[10] H. A. Winston, F. Sun, and B. S. Annigeri. Structural health monitoring with piezoelectric active sensors. In Volume 4: Manufacturing Materials and Metallurgy; Ceramics; Structures and Dynamics; Controls, Diagnostics and Instrumentation; Education, American Society of Mechanical Engineers, GT2000, (2000). https://doi.org/10.1115/2000-gt-0051.
[11] S. Bhalla and C.-K. Soh. Progress in structural health monitoring and non-destructive evaluation using piezo-impedance transducers. In Smart Materials and Structures: New Research, Nova Science Publishers, Inc., New York, (2007), pp. 177–228.
[12] G. Huang, F. Song, and X. Wang. Quantitative modeling of coupled piezo-elastodynamic behavior of piezoelectric actuators bonded to an elastic medium for structural health monitoring: A review. Sensors, 10, (2010), pp. 3681–3702. https://doi.org/10.3390/s100403681.
[13] Z. Shu. Application of piezoelectric materials in structural health monitoring of civil engineering structure. Chemical Engineering Transactions, 59, (2017), pp. 523–528. https://doi.org/10.3303/CET1759088.
[14] W. S. Na and J. Baek. A review of the piezoelectric electromechanical impedance based structural health monitoring technique for engineering structures. Sensors, 18, (2018). https://doi.org/10.3390/s18051307.
[15] Q. Wang and S. T. Quek. Flexural vibration analysis of sandwich beam coupled with piezoelectric actuator. Smart Materials and Structures, 9, (1), (2000). https://doi.org/10.1088/0964- 726/9/1/311.
[16] Q. Wang and S. T. Quek. Enhancing flutter and buckling capacity of column by piezoelectric layers. International Journal of Solids and Structures, 39, (2002), pp. 4167–4180. https://doi.org/10.1016/s0020-7683(02)00334-7.
[17] Q. Wang, W. H. Duan, and S. T. Quek. Repair of notched beam under dynamic load using piezoelectric patch. International Journal of Mechanical Sciences, 46, (2004), pp. 1517–1533. https://doi.org/10.1016/j.ijmecsci.2004.09.012.
[18] S. Zhao, N. Wu, and Q. Wang. Crack identification through scan-tuning of vibration characteristics using piezoelectric materials. Smart Materials and Structures, 26, (2016). https://doi.org/10.1088/1361-665x/aa520a.
[19] S. Ritdumrongkul and Y. Fujino. Identification of the location and size of cracks in beams by a piezoceramic actuator–sensor. Structural Control and Health Monitoring, 14, (6), (2007), pp. 931–943. https://doi.org/10.1002/stc.204.
[20] D. Wang, H. Song, and H. Zhu. Electromechanical impedance analysis on piezoelectric smart beam with a crack based on spectral element method. Mathematical Problems in Engineering, 2015, (2015), pp. 1–13. https://doi.org/10.1155/2015/713501.
[21] T. Wang, B. Tan, M. Lu, Z. Zhang, and G. Lu. Piezoelectric electro-mechanical impedance (EMI) based structural crack monitoring. Applied Sciences, 10, (2020). https://doi.org/10.3390/app10134648.
[22] X.-F. Li. A unified approach for analyzing static and dynamic behaviors of functionally graded Timoshenko and Euler–Bernoulli beams. Journal of Sound and Vibration, 318, (2008), pp. 1210–1229. https://doi.org/10.1016/j.jsv.2008.04.056.
[23] S. A. Sina, H. M. Navazi, and H. Haddadpour. An analytical method for free vibration analysis of functionally graded beams. Materials & Design, 30, (2009), pp. 741–747. https://doi.org/10.1016/j.matdes.2008.05.015.
[24] L. O. Larbi, A. Kaci, M. S. A. Houari, and A. Tounsi. An efficient shear deformation beam theory based on neutral surface position for bending and free vibration of functionally graded beams. Mechanics Based Design of Structures and Machines, 41, (2013), pp. 421–433. https://doi.org/10.1080/15397734.2013.763713.
[25] H. Su and J. R. Banerjee. Development of dynamic stiffness method for free vibration of functionally graded Timoshenko beams. Computers & Structures, 147, (2015), pp. 107–116. https://doi.org/10.1016/j.compstruc.2014.10.001.
[26] X. Wang, X. Liang, and C. Jin. Accurate dynamic analysis of functionally graded beams under a moving point load. Mechanics Based Design of Structures and Machines, 45, (2016), pp. 76–91. https://doi.org/10.1080/15397734.2016.1145060.
[27] J. Yang and Y. Chen. Free vibration and buckling analyses of functionally graded beams with edge cracks. Composite Structures, 83, (2008), pp. 48–60. https://doi.org/10.1016/j.compstruct.2007.03.006.
[28] S¸ . D. Akbas¸. Free vibration characteristics of edge cracked functionally graded beams by using finite element method. International Journal of Engineering Trends and Technology, 4, (10), (2013), pp. 4590–4597.
[29] K. Aydin. Free vibration of functionally graded beams with arbitrary number of surface cracks. European Journal of Mechanics - A/Solids, 42, (2013), pp. 112–124. https://doi.org/10.1016/j.euromechsol.2013.05.002.
[30] N. T. Khiem, H. T. Tran, and D. Nam. Modal analysis of cracked continuous Timoshenko beam made of functionally graded material. Mechanics Based Design of Structures and Machines, 48, (2019), pp. 459–479. https://doi.org/10.1080/15397734.2019.1639518.
[31] Z. Yu and F. Chu. Identification of crack in functionally graded material beams using the p-version of finite element method. Journal of Sound and Vibration, 325, (2009), pp. 69–84. https://doi.org/10.1016/j.jsv.2009.03.010.
[32] A. Banerjee, B. Panigrahi, and G. Pohit. Crack modelling and detection in Timoshenko FGM beam under transverse vibration using frequency contour and response surface model with GA. Nondestructive Testing and Evaluation, 31, (2015), pp. 142–164. https://doi.org/10.1080/10589759.2015.1071812.
[33] N. T. Khiem and N. N. Huyen. A method for crack identification in functionally graded Timoshenko beam. Nondestructive Testing and Evaluation, 32, (2016), pp. 319–341. https://doi.org/10.1080/10589759.2016.1226304.
[34] M. K. Khorramabadi and A. R. Nezamabadi. Stability of functionally graded beams with piezoelectric layers based on the first order shear deformation theory. International Journal of Electrical and Computer Engineering, 4, (11), (2010), pp. 1641–1644.
[35] Y. S. Li, W. J. Feng, and Z. Y. Cai. Bending and free vibration of functionally graded piezoelectric beam based on modified strain gradient theory. Composite Structures, 115, (2014), pp. 41– 50. https://doi.org/10.1016/j.compstruct.2014.04.005.
[36] K. Bendine, F. B. Boukhoulda, M. Nouari, and Z. Satla. Active vibration control of functionally graded beams with piezoelectric layers based on higher order shear deformation theory. Earthquake Engineering and Engineering Vibration, 15, (2016), pp. 611–620. https://doi.org/10.1007/s11803-016-0352-y.
[37] N. T. Khiem, T. T. Hai, and L. Q. Huong. Effect of piezoelectric patch on natural frequencies of Timoshenko beam made of functionally graded material. Materials Research Express, 7, (2020). https://doi.org/10.1088/2053-1591/ab8df5.
[38] N. T. Khiem, D. T. Huan, and T. T. Hieu. Vibration of cracked FGM beam with piezoelectric layer under moving load. Journal of Vibration Engineering & Technologies, 11, (2022), pp. 755–769. https://doi.org/10.1007/s42417-022-00607-8.
[39] N. T. Khiem, N. N. Huyen, and N. T. Long. Vibration of cracked Timoshenko beam made of functionally graded material. In Conference Proceedings of the Society for Experimental Mechanics Series, Springer International Publishing, (2017), pp. 133–143. https://doi.org/10.1007/978-3-319-54735-015.
[40] T. T. Hai, P. T. Hang, and N. T. Khiem. A novel criterion for crack identification in beamlike structures using distributed piezoelectric sensor and controlled moving load. Journal of Sound and Vibration, 572, (2024). https://doi.org/10.1016/j.jsv.2023.118155.
Downloads
Published
How to Cite
License

This work is licensed under a Creative Commons Attribution-ShareAlike 4.0 International License.









