Three versions of Galerkin's method applied to the static deflection of a stepped beam
Author affiliations
DOI:
https://doi.org/10.15625/0866-7136/20647Keywords:
stepped beams, Galerkin’s method, generalized functionsAbstract
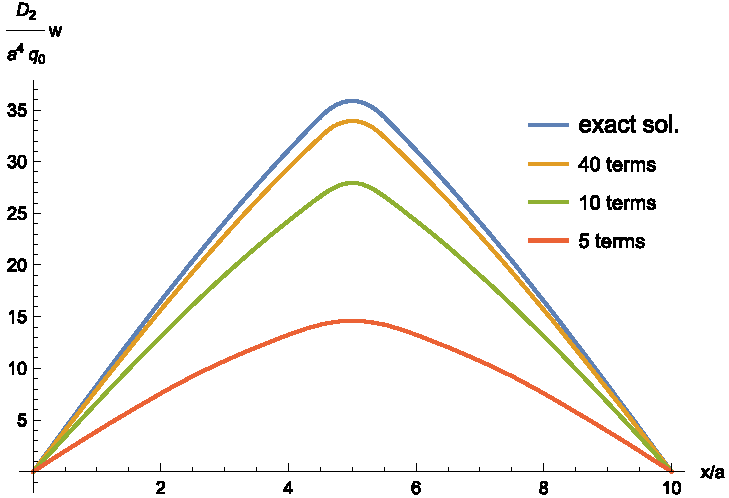
This work deals with the application of Galerkin's method for stepped structures to evaluate the static deflection under distributed loading. In this study, we compare two different implementations of the well-known method to the exact analytical result in order to prove that only the second method is able to give a good approximation to the solution of the problem.
Downloads
References
B. G. Galerkin. Sterzhni i plastiny. Ryady v nekotorykh voprosakh uprugogo ravnovesiya sterzhnei i plastin (Rods and plates series occuring in some problems of elastic equilibrium of rods and plates). Vestnik Inzhenerov i Tekhnikov, Petrograd, 19, (1915), pp. 897–908. (in Russian) (English Translation: 63-18925, Clearinghouse Fed. Sci. Tech. Info. 1963).
S. G. Mikhlin. The numerical performance of variational methods. Wolters-Noordhoff Publishing, Groningen, (1971).
H. Leipholz. Use of Galerkins method for vibration problems. The Shock and Vibration Digest, 8, (1976), pp. 3–18.
H. H. E. Leipholz and R. Mandadi. On the non-uniform convergence of Galerkin’s method. Journal of Sound and Vibration, 57, (1978), pp. 483–498.
H. Leipholz. Über dieWahl der Ansatzfunktionen bei der Durchführung des Verfahrens von Galerkin. Acta Mechanica, 3, (1967), pp. 295–317.
H. H. E. Leipholz. On the convergence of Ritz and Galerkin’s method in the case of certain nonconservative systems and using admissible coordinate functions. Acta Mechanica, 19, (1974), pp. 57–76.
J. Singer. On the equivalence of the Galerkin and Rayleigh-Ritz methods. The Journal of the Royal Aeronautical Society, 66, (1962), pp. 592–592.
C. D. Bailey. The Galerkin formulation and the Hamilton-Ritz formulation: A comparison. Acta Mechanica, 36, (1980), pp. 63–70.
M. J. Gander and G. Wanner. From Euler, Ritz, and Galerkin to modern computing. SIAM Review, 54, (2012), pp. 627–666.
S. Repin. One hundred years of the Galerkin method. Computational Methods in Applied Mathematics, 17, (2017), pp. 351–357.
B. N. Bastatsky and A. R. Khvoles. On some specifics of applying Bubnov-Galerkin method to practical analysis of structures. Stroitelnaya Mekhanika i Raschet Sooruzhenii, (Structural Mechanics and Analysis of Constructions), (2), (1972), pp. 55–59. (in Russian).
D. V. Vainberg and I. Z. Roitfarb. Analysis of plates and shells with discontinuous parameters. In Raschet Prostranstvennykh Konstrukzii (Analysis of Space Structures), Moscow: ”Stroiizdat” Publishing House, Vol. 10, (1965), pp. 38–80. (in Russian).
C. Maurini, M. Porfiri, and J. Pouget. Numerical methods for modal analysis of stepped piezoelectric beams. Journal of Sound and Vibration, 298, (2006), pp. 918–933.
I. Elishakoff, A. P. Ankitha, and A. Marzani. Rigorous versus na¨ıve implementation of the Galerkin method for stepped beams. Acta Mechanica, 230, (2019), pp. 3861–3873.
I. Elishakoff, M. Amato, A. P. Ankitha, and A. Marzani. Rigorous implementation of the Galerkin method for stepped structures needs generalized functions. Journal of Sound and Vibration, 490, (2021).
I. Elishakoff, M. Amato, and A. Marzani. Galerkin’s method revisited and corrected in the problem of Jaworski and Dowell. Mechanical Systems and Signal Processing, 155, (2021).
M. Amato, I. Elishakoff, and J. N. Reddy. Flutter of a multicomponent beam in a supersonic flow. AIAA Journal, 59, (2021), pp. 4342–4353.
D. Avalos, H. Hack, and P. A. A. Laura. Galerkin method and axisymmetric vibrations of polar-orthotropic circular plates. AIAA Journal, 20, (1982), pp. 1626–1628.
T. Toulorge and W. Desmet. Curved boundary treatments for the discontinuous Galerkin method applied to aeroacoustic propagation. AIAA Journal, 48, (2010), pp. 479–489.
I. S. Raju and D. R. Phillips. Local coordinate approach in meshless local Petrov-Galerkin method for beam problems. AIAA Journal, 41, (2003), pp. 975–978.
A. W. Leissa, W. E. Clause, L. E. Hulbert, and A. T. Hopper. A comparison of approximate methods for the solution of plate bending problems. AIAA Journal, 7, (1969), pp. 920–928.
B. T. Helenbrook and H. L. Atkins. Application of p-multigrid to discontinuous Galerkin formulations of the Poisson equation. AIAA Journal, 44, (2006), pp. 566–575.
P. J. Blonigan, F. Rizzi, M. Howard, J. A. Fike, and K. T. Carlberg. Model reduction for steady hypersonic aerodynamics via conservative manifold least-squares Petrov–Galerkin projection. AIAA Journal, 59, (2021), pp. 1296–1312.
Downloads
Published
How to Cite
License

This work is licensed under a Creative Commons Attribution-ShareAlike 4.0 International License.









