Dynamic response of sandwich beam with porous core excited by two harmonic loads travelling in opposite directions
Author affiliations
DOI:
https://doi.org/10.15625/0866-7136/20580Keywords:
sandwich porous beam, moving harmonic load, Navier solution, dynamic responseAbstract
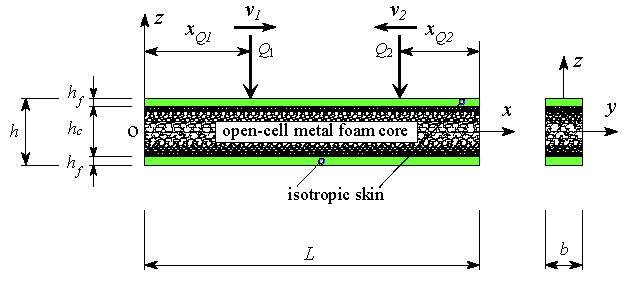
This paper presents the time history response of a sandwich beam with a porous core subjected to two moving harmonic loads with opposite directions. In the modelling, the beam is combined of two isotropic face sheets and a porous core with symmetric porosity distribution. The quasi-3D shear deformation beam theory in conjunction with Hamilton's variational principle is utilized to set up the governing equations of motion. The Navier solution is used to obtain the displacement field. The accuracy of the study is validated by comparing with existing results in the literature for specific cases. Effects of the velocity and excitation frequency of the moving loads on the deflection-time history are investigated and discussed. Numerical results reveal that in the case of the double-moving harmonic loads in the antiphase, the resonance phenomenon cannot occur when the excitation frequency approaches the natural frequency of the beam.
Downloads
References
N. E. P. A. Gokhale and B. Basu. Light weighting for defense, aerospace, and transportation. Springer Singapore, (2019).
M. F. Ashby, A. Evans, N. A. Fleck, L. J. Gibson, J. W. Hutchinson, H. N. G. Wadley, and F. Delale. Metal foams: A design guide. Applied Mechanics Reviews, 54, (2001), pp. B105–B106.
D. Chen, S. Kitipornchai, and J. Yang. Nonlinear free vibration of shear deformable sandwich beam with a functionally graded porous core. Thin-Walled Structures, 107, (2016), pp. 39–48. https:/doi.org/10.1016/j.tws.2016.05.025.
Y. Wang, H. Ma, K. Xie, T. Fu, J. Chen, and Y. Liu. Nonlinear bending of a sandwich beam with metal foam and GPLRC face-sheets using Chebyshev–Ritz method: Effects of agglomeration and internal pore. Thin-Walled Structures, 181, (2022).
B. Srikarun, W. Songsuwan, and N. Wattanasakulpong. Linear and nonlinear static bending of sandwich beams with functionally graded porous core under different distributed loads. Composite Structures, 276, (2021).
Y. Q. Wang and H. L. Zhao. Free vibration analysis of metal foam core sandwich beams on elastic foundation using Chebyshev collocation method. Archive of Applied Mechanics, 89, (2019), pp. 2335–2349.
A. Garg, H. D. Chalak, M. O. Belarbi, and A. M. Zenkour. A parametric analysis of free vibration and bending behavior of sandwich beam containing an open-cell metal foam core. Archives of Civil and Mechanical Engineering, 22, (2022).
L. H. Zhang, S. K. Lai, C. Wang, and J. Yang. DSC regularized Dirac-delta method for dynamic analysis of FG graphene platelet-reinforced porous beams on elastic foundation under a moving load. Composite Structures, 255, (2021).
W. Songsuwan, N. Wattanasakulpong, and S. Kumar. Nonlinear transient response of sandwich beams with functionally graded porous core under moving load. Engineering Analysis with Boundary Elements, 155, (2023), pp. 11–24.
M. Şimşek. Vibration analysis of a functionally graded beam under a moving mass by using different beam theories. Composite Structures, 92, (2010), pp. 904–917.
P. Jafari and Y. Kiani. A four-variable shear and normal deformable quasi-3D beam model to analyze the free and forced vibrations of FG-GPLRC beams under moving load. Acta Mechanica, 233, (2022), pp. 2797–2814.
V.-L. Nguyen, M.-T. Tran, T.-B. Chu, T.-A. Nguyen, and V.-L. Nguyen. Nonlinear dynamic response of functionally graded porous beams under a moving mass using Reddy’s beam theory. Iranian Journal of Science and Technology, Transactions of Mechanical Engineering, (2023), pp. 1–17.
M. H. Yas and M. Heshmati. Dynamic analysis of functionally graded nanocomposite beams reinforced by randomly oriented carbon nanotube under the action of moving load. Applied Mathematical Modelling, 36, (2012), pp. 1371–1394.
M. Heshmati and M. H. Yas. Dynamic analysis of functionally graded multi-walled carbon nanotube-polystyrene nanocomposite beams subjected to multi-moving loads. Materials & Design, 49, (2013), pp. 894–904.
N. Wattanasakulpong, A. Karamanli, and T. P. Vo. Nonlinear dynamic response of FG-GPLRC beams induced by two successive moving loads. Engineering Analysis with Boundary Elements, 159, (2024), pp. 164–179.
M. Şimşek and M. Al-shujairi. Static, free and forced vibration of functionally graded (FG) sandwich beams excited by two successive moving harmonic loads. Composites Part B: Engineering, 108, (2017), pp. 18–34.
A. Sayyidmousavi, M. Foroutan, and Z. Fawaz. Meshfree dynamic analysis of functionally graded carbon nanotube reinforced polymer sandwich beams under harmonic moving loads. Australian Journal of Mechanical Engineering, (2022), pp. 1–13.
A. S. Sayyad and Y. M. Ghugal. Modeling and analysis of functionally graded sandwich beams: a review. Mechanics of Advanced Materials and Structures, 26, (2018), pp. 1776–1795.
J. N. Reddy. Mechanics of laminated composite plates and shells. CRC Press, (2003).
M. M. Stanis̆ić and J. C. Hardin. On the response of beams to an arbitrary number of concentrated moving masses. Journal of the Franklin Institute, 287, (1969), pp. 115–123.
Downloads
Published
How to Cite
License

This work is licensed under a Creative Commons Attribution-ShareAlike 4.0 International License.
Funding data
-
National Foundation for Science and Technology Development
Grant numbers 107.02-2021.16









