Exact receptance function of a tapered AFG beam with nonlinearly varying ratios of beam properties carrying concentrated masses
Author affiliations
DOI:
https://doi.org/10.15625/0866-7136/19697Keywords:
receptance, frequency response function, concentrated mass, functionally graded material beamAbstract
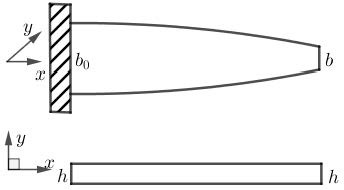
This paper presents a method for establishing the exact receptance function of a tapered axially functionally graded (AFG) beam with nonlinear ratios of properties using the Adomian method. In current papers, the Adomian method was applied for linearly tapered beams where the geometric series was used conveniently. However, for nonuniform AFG beams with nonlinearly varying ratios of properties, the geometric series cannot be used, thus the other type of power series needs to be established and applied. In this paper, the derivation of the power series applied for obtaining the exact receptance function of a nonuniform AFG beam with nonlinearly varying ratios of properties is presented. Numerical simulation results of the receptance function of a tapered AFG beam with nonlinearly varying ratios of beam properties carrying concentrated masses are conducted and provided. The influences of the concentrated masses and the varying ratios of properties of beam on the receptance matrix are also investigated and presented.
Downloads
Metrics
References
M. Ghandchi Tehrani, R. N. R. Elliott, and J. E. Mottershead. Partial pole placement in structures by the method of receptances: Theory and experiments. Journal of Sound and Vibration, 329, (2010), pp. 5017–5035. DOI: https://doi.org/10.1016/j.jsv.2010.06.018
J. E. Mottershead. On the zeros of structural frequency response functions and their sensitivities. Mechanical Systems and Signal Processing, 12, (1998), pp. 591–597. DOI: https://doi.org/10.1006/mssp.1998.0167
Z. Wang, R. M. Lin, and M. K. Lim. Structural damage detection using measured FRF data. Computer Methods in Applied Mechanics and Engineering, 147, (1997), pp. 187–197. DOI: https://doi.org/10.1016/S0045-7825(97)00013-3
M. Gürgöze and H. Erol. Determination of the frequency response function of a cantilevered beam simply supported in-span. Journal of Sound and Vibration, 247, (2001), pp. 372–378. DOI: https://doi.org/10.1006/jsvi.2000.3618
Q. Huang, Y. L. Xu, J. C. Li, Z. Q. Su, and H. J. Liu. Structural damage detection of controlled building structures using frequency response functions. Journal of Sound and Vibration, 331, (2012), pp. 3476–3492. DOI: https://doi.org/10.1016/j.jsv.2012.03.001
L. Li, Y. Hu, X. Wang, and L. Lü. A hybrid expansion method for frequency response functions of non-proportionally damped systems. Mechanical Systems and Signal Processing, 42, (2014), pp. 31–41. DOI: https://doi.org/10.1016/j.ymssp.2013.07.020
G. Failla. An exact generalised function approach to frequency response analysis of beams and plane frames with the inclusion of viscoelastic damping. Journal of Sound and Vibration, 360, (2016), pp. 171–202. DOI: https://doi.org/10.1016/j.jsv.2015.09.006
K. V. Nguyen, T. T. B. Dao, and M. Van Cao. Comparison studies of the receptance matrices of the isotropic homogeneous beam and the axially functionally graded beam carrying concentrated masses. Applied Acoustics, 160, (2020). DOI: https://doi.org/10.1016/j.apacoust.2019.107160
K. V. Singh, C. Black, and R. Kolonay. Active aeroelastic output feedback control with partial measurements by the method of receptances. Aerospace Science and Technology, 86, (2019), pp. 47–63. DOI: https://doi.org/10.1016/j.ast.2018.12.037
S. Lenci, F. Clementi, and C. E. N. Mazzilli. Simple formulas for the natural frequencies of non-uniform cables and beams. International Journal of Mechanical Sciences, 77, (2013), pp. 155–163. DOI: https://doi.org/10.1016/j.ijmecsci.2013.09.028
R. Eberle and M. Oberguggenberger. A new method for estimating the bending stiffness curve of non-uniform Euler-Bernoulli beams using static deflection data. Applied Mathematical Modelling, 105, (2022), pp. 514–533. DOI: https://doi.org/10.1016/j.apm.2021.12.042
S. Hadian Jazi, M. Hadian, and K. Torabi. An exact closed-form explicit solution of free transverse vibration for non-uniform multi-cracked beam. Journal of Sound and Vibration, 570, (2024). DOI: https://doi.org/10.1016/j.jsv.2023.117986
Q. S. Li. Free vibration analysis of non-uniform beams with an arbitrary number of cracks and concentrated masses. Journal of Sound and Vibration, 252, (2002), pp. 509–525. DOI: https://doi.org/10.1006/jsvi.2001.4034
M. A. Mahmoud. Natural frequency of axially functionally graded, tapered cantilever beams with tip masses. Engineering Structures, 187, (2019), pp. 34–42. DOI: https://doi.org/10.1016/j.engstruct.2019.02.043
M. A. Mahmoud. Free vibrations of tapered and stepped, axially functionally graded beams with any number of attached masses. Engineering Structures, 267, (2022). DOI: https://doi.org/10.1016/j.engstruct.2022.114696
G. Tan, Y. Liu, Y. Gong, Y. Shen, and Z. Liu. Free vibration of the cracked non-uniform beam with cross section varying as polynomial functions. KSCE Journal of Civil Engineering, 22, (2018), pp. 4530–4546. DOI: https://doi.org/10.1007/s12205-018-1833-5
Downloads
Published
How to Cite
License
This work is licensed under a Creative Commons Attribution-ShareAlike 4.0 International License.
Funding data
-
Vietnam Academy of Science and Technology
Grant numbers ĐLTE00.03/23-24
