An edge-based smoothed finite element for buckling analysis of functionally graded material variable-thickness plates
Author affiliations
DOI:
https://doi.org/10.15625/0866-7136/15503Keywords:
buckling analysis, critical load, variable thickness plate, edge-based finite element method, ES-MITC3Abstract
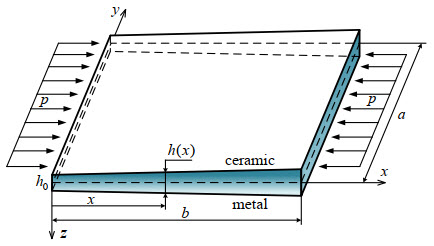
The paper aims to extend the ES-MITC3 element, which is an integration of the edge-based smoothed finite element method (ES-FEM) with the mixed interpolation of tensorial components technique for the three-node triangular element (MITC3 element), for the buckling analysis of the FGM variable-thickness plates subjected to mechanical loads. The proposed ES-MITC3 element is performed to eliminate the shear locking phenomenon and to enhance the accuracy of the existing MITC3 element. In the ES-MITC3 element, the stiffness matrices are obtained by using the strain smoothing technique over the smoothing domains formed by two adjacent MITC3 triangular elements sharing the same edge. The numerical results demonstrated that the proposed method is reliable and more accurate than some other published solutions in the literature. The influences of some geometric parameters, material properties on the stability of FGM variable-thickness plates are examined in detail.
Downloads
Metrics
References
I. Ramu and S. C. Mohanty. Buckling analysis of rectangular functionally graded material plates under uniaxial and biaxial compression load. Procedia Engineering, 86, (2014), pp. 748–757.
DOI: https://doi.org/10.1016/j.proeng.2014.11.094
R. Saha and P. R. Maiti. Buckling of simply supported FGM plates under uniaxial load. International Journal of Civil & Structural Engineering, 2, (4), (2012), pp. 1035–1050.
T.-L. Wu, K. K. Shukla, and J. H. Huang. Post-buckling analysis of functionally graded rectangular plates. Composite Structures, 81, (2007), pp. 1–10.
DOI: https://doi.org/10.1016/j.compstruct.2005.08.026
R. Javaheri and M. R. Eslami. Buckling of functionally graded plates under inplane compressive loading. Journal of Applied Mathematics and Mechanics, 82, (2002).
DOI: https://doi.org/10.1002/1521-4001(200204)82:4<277::AID-ZAMM277>3.0.CO;2-Y
A. M. Zenkour. A comprehensive analysis of functionally graded sandwich plates: Part 2—Buckling and free vibration. International Journal of Solids and Structures, 42, (2005), pp. 5243–5258.
DOI: https://doi.org/10.1016/j.ijsolstr.2005.02.016
B. A. S. Shariat and M. R. Eslami. Buckling of thick functionally graded plates under mechanical and thermal loads. Composite Structures, 78, (2007), pp. 433–439.
DOI: https://doi.org/10.1016/j.compstruct.2005.11.001
H.-T. Thai and D.-H. Choi. An efficient and simple refined theory for buckling analysis of functionally graded plates. Applied Mathematical Modelling, 36, (2012), pp. 1008–1022.
DOI: https://doi.org/10.1016/j.apm.2011.07.062
B. S. Reddy, J. S. Kumar, C. E. Reddy, and K. V. K. Reddy. Buckling analysis of functionally graded material plates using higher order shear deformation theory. Journal of Composites, 2013, (2013), pp. 1–12.
DOI: https://doi.org/10.1155/2013/808764
T. I. Thinh, T. M. Tu, T. H. Quoc, and N. V. Long. Vibration and buckling analysis of functionally graded plates using new eight-unknown higher order shear deformation theory. Latin American Journal of Solids and Structures, 13, (2016), pp. 456–477.
DOI: https://doi.org/10.1590/1679-78252522
P.-T. Thang, T. Nguyen-Thoi, and J. Lee. Closed-form expression for nonlinear analysis of imperfect sigmoid-FGM plates with variable thickness resting on elastic medium. Composite Structures, 143, (2016), pp. 143–150.
DOI: https://doi.org/10.1016/j.compstruct.2016.02.002
M. Eisenberger and A. Alexandrov. Buckling loads of variable thickness thin isotropic plates. Thin-Walled Structures, 41, (2003), pp. 871–889.
DOI: https://doi.org/10.1016/S0263-8231(03)00027-2
M. H. Naei, A. Masoumi, and A. Shamekhi. Buckling analysis of circular functionally graded material plate having variable thickness under uniform compression by finite-element method. Proceedings of the Institution of Mechanical Engineers, Part C: Journal of Mechanical Engineering Science, 221, (2007), pp. 1241–1247.
DOI: https://doi.org/10.1243/09544062JMES636
S. K. Jalali, M. H. Naei, and A. Poorsolhjouy. Thermal stability analysis of circular functionally graded sandwich plates of variable thickness using pseudo-spectral method. Materials & Design, 31, (2010), pp. 4755–4763.
DOI: https://doi.org/10.1016/j.matdes.2010.05.009
M. M. Alipour and M. Shariyat. Semi-analytical buckling analysis of heterogeneous variable thickness viscoelastic circular plates on elastic foundations. Mechanics Research Communications, 38, (2011), pp. 594–601.
DOI: https://doi.org/10.1016/j.mechrescom.2011.09.001
M. M. Alipour and M. Shariyat. Semianalytical Solution for Buckling Analysis of Variable Thickness Two-Directional Functionally Graded Circular Plates with Nonuniform Elastic Foundations. Journal of Engineering Mechanics, 139, (2013), pp. 664–676.
DOI: https://doi.org/10.1061/(ASCE)EM.1943-7889.0000522
F. Alinaghizadeh and M. Shariati. Buckling Analysis of Variable Thickness Radially Functionally Graded Annular Sector Plates Resting on Two-Parameter Elastic Foundations by the GDQ Method. International Journal of Applied Mechanics, 07, (2015).
DOI: https://doi.org/10.1142/S1758825115500830
O. Bouguenina, K. Belakhdar, A. Tounsi, and E. A. Adda Bedia. Numerical analysis of FGM plates with variable thickness subjected to thermal buckling. Steel and Composite Structures, 19, (3), (2015), pp. 679–695.
DOI: https://doi.org/10.12989/scs.2015.19.3.679
F. Benlahcen and K. Belakhdar. Thermal buckling resistance of simply supported FGM plates with parabolic-concave thickness variation. Steel and Composite Structures, 29, (5), (2018), pp. 591–602.
P. P. Minh and N. D. Duc. The effect of cracks on the stability of the functionally graded plates with variable-thickness using HSDT and phase-field theory. Composites Part B: Engineering, 175, (2019).
DOI: https://doi.org/10.1016/j.compositesb.2019.107086
A. M. Zenkour. Bending of thin rectangular plates with variable-thickness in a hygrothermal environment. Thin-Walled Structures, 123, (2018), pp. 333–340.
DOI: https://doi.org/10.1016/j.tws.2017.11.038
M. N. M. Allam, R. Tantawy, and A. M. Zenkour. Thermoelastic stresses in functionally graded rotating annular disks with variable thickness. Journal of Theoretical and Applied Mechanics, (2018).
DOI: https://doi.org/10.15632/jtam-pl.56.4.1029
T. Banh-Thien, H. Dang-Trung, L. Le-Anh, V. Ho-Huu, and T. Nguyen-Thoi. Buckling analysis of non-uniform thickness nanoplates in an elastic medium using the isogeometric analysis. Composite Structures, 162, (2017), pp. 182–193.
DOI: https://doi.org/10.1016/j.compstruct.2016.11.092
P.-S. Lee and K.-J. Bathe. Development of MITC isotropic triangular shell finite elements. Computers & Structures, 82, (2004), pp. 945–962.
DOI: https://doi.org/10.1016/j.compstruc.2004.02.004
G. R. Liu, T. Nguyen-Thoi, and K. Y. Lam. An edge-based smoothed finite element method (ES-FEM) for static, free and forced vibration analyses of solids. Journal of Sound and Vibration, 320, (2009), pp. 1100–1130.
DOI: https://doi.org/10.1016/j.jsv.2008.08.027
T. Chau-Dinh, Q. Nguyen-Duy, and H. Nguyen-Xuan. Improvement on MITC3 plate finite element using edge-based strain smoothing enhancement for plate analysis. Acta Mechanica, 228, (2017), pp. 2141–2163.
DOI: https://doi.org/10.1007/s00707-017-1818-3
T.-K. Nguyen, V.-H. Nguyen, T. Chau-Dinh, T. P. Vo, and H. Nguyen-Xuan. Static and vibration analysis of isotropic and functionally graded sandwich plates using an edgebased MITC3 finite elements. Composites Part B: Engineering, 107, (2016), pp. 162–173.
DOI: https://doi.org/10.1016/j.compositesb.2016.09.058
Q.-H. Pham, T.-V. Tran, T.-D. Pham, and D.-H. Phan. An Edge-Based Smoothed MITC3 (ESMITC3) Shell Finite Element in Laminated Composite Shell Structures Analysis. International Journal of Computational Methods, 15, (2018).
DOI: https://doi.org/10.1142/S0219876218500603
Q.-H. Pham, T.-D. Pham, Q. V. Trinh, and D.-H. Phan. Geometrically nonlinear analysis of functionally graded shells using an edge-based smoothed MITC3 (ESMITC3) finite elements. Engineering with Computers, 36, (3), (2020), pp. 1069–1082.
DOI: https://doi.org/10.1007/s00366-019-00750-z
D. Pham-Tien, H. Pham-Quoc, V. Tran-The, T. Vu-Khac, and N. Nguyen-Van. Transient Analysis of Laminated Composite Shells Using an Edge-Based Smoothed Finite Element Method. In Proceedings of the International Conference on Advances in Computational Mechanics 2017, Springer Singapore, (2018), pp. 1075–1094.
DOI: https://doi.org/10.1007/978-981-10-7149-2_75
T. T. Tran, Q.-H. Pham, and T. Nguyen-Thoi. An Edge-Based Smoothed Finite Element for Free Vibration Analysis of Functionally Graded Porous (FGP) Plates on Elastic Foundation Taking into Mass (EFTIM). Mathematical Problems in Engineering, 2020, (2020), pp. 1–17.
DOI: https://doi.org/10.1155/2020/8278743
K.-U. Bletzinger, M. Bischoff, and E. Ramm. A unified approach for shear-locking-free triangular and rectangular shell finite elements. Computers & Structures, 75, (2000), pp. 321–334.
DOI: https://doi.org/10.1016/S0045-7949(99)00140-6
T. Nguyen-Thoi, P. Phung-Van, H. Nguyen-Xuan, and C. Thai-Hoang. A cell-based smoothed discrete shear gap method using triangular elements for static and free vibration analyses of Reissner-Mindlin plates. International Journal for Numerical Methods in Engineering, 91, (2012), pp. 705–741.
DOI: https://doi.org/10.1002/nme.4289
K.-J. Bathe and E. N. Dvorkin. A formulation of general shell elements—the use of mixed interpolation of tensorial components. International Journal for Numerical Methods in Engineering, 22, (1986), pp. 697–722.
DOI: https://doi.org/10.1002/nme.1620220312
Downloads
Published
How to Cite
Issue
Section
License
This work is licensed under a Creative Commons Attribution-ShareAlike 4.0 International License.
Funding data
-
National Foundation for Science and Technology Development
Grant numbers 107.02-2019.330
