Size-dependent free vibration of porous piezoelectric microplate resting on an elastic substrate using MSGT, HSDT, and IGA
Author affiliations
DOI:
https://doi.org/10.15625/0866-7136/23029Keywords:
piezoelectric microplate, isogeometric approach, modified strain gradient theory, higher-order shear deformation theory, elastic foundationAbstract
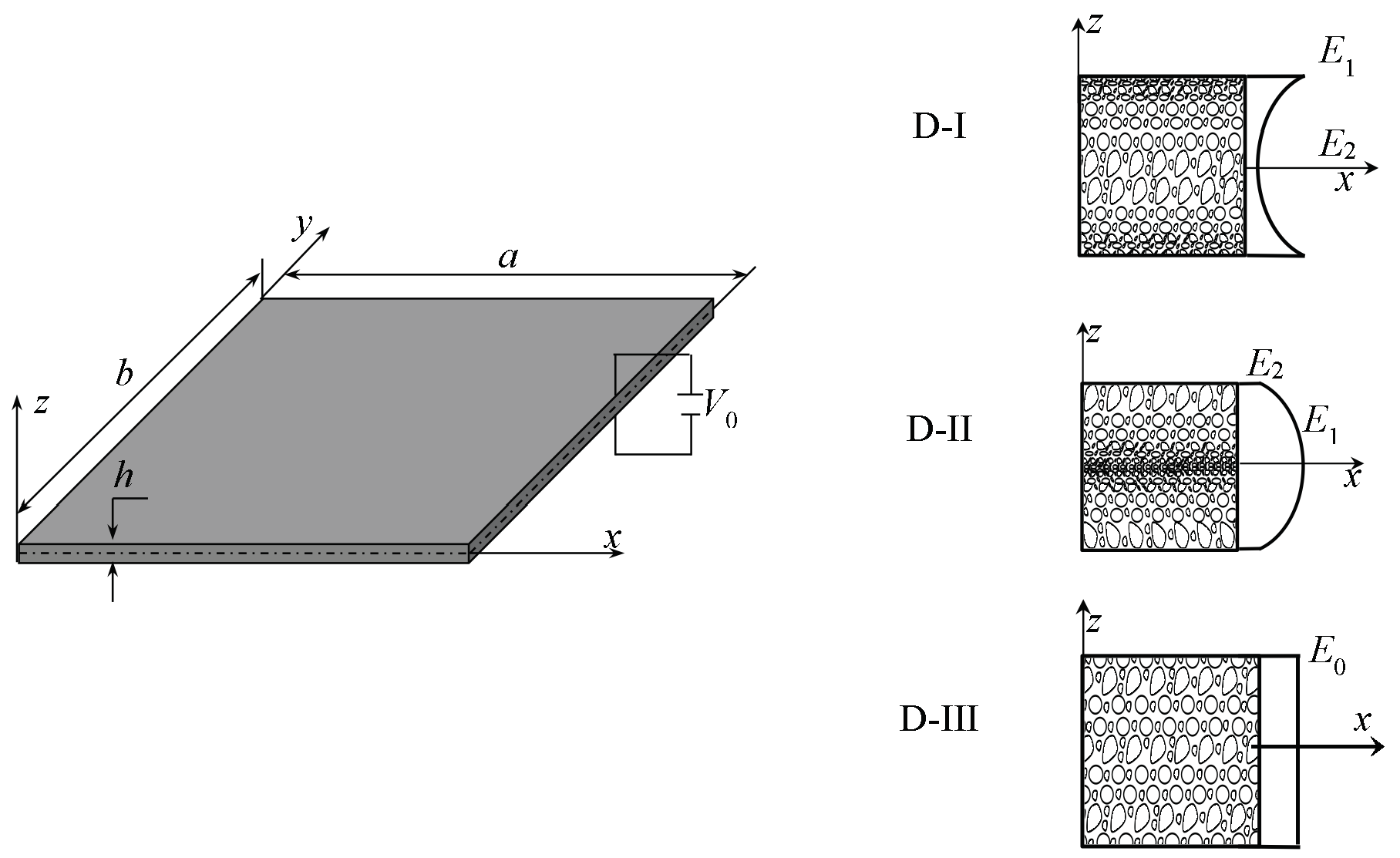
This work presents the first comprehensive study combining higher-order shear deformation theory (HSDT), modified strain gradient theory (MSGT), and the isogeometric approach (IGA) to investigate the size-dependent free vibration behavior of functionally graded porous piezoelectric (FGPP) microplates. The microplate is composed of a piezoelectric material, with porosity distributed across the thickness following three distinct patterns: symmetric I, symmetric II, and uniform. Hamilton's principle, combined with HSDT and MSGT, is employed to derive the governing equations of the piezoelectric microplate. The natural frequencies of the FGPP microplates are obtained by solving the explicit governing equations using the isogeometric analysis approach. Furthermore, the effects of length scale parameters, porosity distribution patterns, porosity coefficient, external electric voltage, and boundary conditions on the vibrational behavior of the FGPP microplate are thoroughly investigated. The proposed method offers accurate size-dependent predictions and provides new reference solutions for the optimal design of advanced piezoelectric microstructures.
Downloads
References
[1] D. C. C. Lam, F. Yang, A. C. M. Chong, J. Wang, and P. Tong. Experiments and theory in strain gradient elasticity. Journal of the Mechanics and Physics of Solids, 51, (2003), pp. 1477– 1508. https://doi.org/10.1016/s0022-5096(03)00053-x.
[2] T. T. Tran and D. K. Nguyen. Vibration of agglomerated CNTRC micro-scale beams carrying a moving concentrated load. Vietnam Journal of Mechanics, 46, (2024), pp. 265–281. https://doi.org/10.15625/0866-7136/21064.
[3] B. Zhang, Y. He, D. Liu, L. Shen, and J. Lei. An efficient size-dependent plate theory for bending, buckling and free vibration analyses of functionally graded microplates resting on elastic foundation. Applied Mathematical Modelling, 39, (2015), pp. 3814–3845. https://doi.org/10.1016/j.apm.2014.12.001.
[4] M. Kandaz and H. Dal. A comparative study of modified strain gradient theory and modified couple stress theory for gold microbeams. Archive of Applied Mechanics, 88, (2018), pp. 2051– 2070. https://doi.org/10.1007/s00419-018-1436-0.
[5] B. Wang, S. Zhou, J. Zhao, and X. Chen. A size-dependent Kirchhoff micro-plate model based on strain gradient elasticity theory. European Journal of Mechanics - A/Solids, 30, (2011), pp. 517–524. https://doi.org/10.1016/j.euromechsol.2011.04.001.
[6] R. Ansari, M. F. Shojaei, V. Mohammadi, R. Gholami, and H. Rouhi. Size-dependent thermal buckling and postbuckling of functionally graded annular microplates based on the modified strain gradient theory. Journal of Thermal Stresses, 37, (2014), pp. 174–201. https://doi.org/10.1080/01495739.2013.839767.
[7] R. Ansari, R. Gholami, M. Faghih Shojaei, V. Mohammadi, and S. Sahmani. Bending, buckling and free vibration analysis of size-dependent functionally graded circular/annular microplates based on the modified strain gradient elasticity theory. European Journal of Mechanics - A/Solids, 49, (2015), pp. 251–267. https://doi.org/10.1016/j.euromechsol.2014.07.014.
[8] A. Karamanli and T. P. Vo. A quasi-3D theory for functionally graded porous microbeams based on the modified strain gradient theory. Composite Structures, 257, (2021). https://doi.org/10.1016/j.compstruct.2020.113066.
[9] X.-H. Wu, C. Chen, Y.-P. Shen, and X.-G. Tian. A high order theory for functionally graded piezoelectric shells. International Journal of Solids and Structures, 39, (2002), pp. 5325–5344. https://doi.org/10.1016/s0020-7683(02)00418-3.
[10] H. Tanzadeh and H. Amoushahi. Buckling and free vibration analysis of piezoelectric laminated composite plates using various plate deformation theories. European Journal of Mechanics - A/Solids, 74, (2019), pp. 242–256. https://doi.org/10.1016/j.euromechsol.2018.11.013.
[11] X.-L. Huang and H.-S. Shen. Vibration and dynamic response of functionally graded plates with piezoelectric actuators in thermal environments. Journal of Sound and Vibration, 289, (2006), pp. 25–53. https://doi.org/10.1016/j.jsv.2005.01.033.
[12] Z. Yan and L. Y. Jiang. Surface effects on the vibration and buckling of piezoelectric nanoplates. EPL (Europhysics Letters), 99, (2012). https://doi.org/10.1209/0295-5075/99/27007.
[13] Y. Tadi Beni. Size-dependent electromechanical bending, buckling, and free vibration analysis of functionally graded piezoelectric nanobeams. Journal of Intelligent Material Systems and Structures, 27, (2016), pp. 2199–2215. https://doi.org/10.1177/1045389x15624798.
[14] Y. Ren and H. Qing. Elastic buckling and free vibration of functionally graded piezoelectric nanobeams using nonlocal integral models. International Journal of Structural Stability and Dynamics, 22, (2022). https://doi.org/10.1142/s021945542250047x.
[15] F. Ebrahimi, A. Rastgoo, and M. N. Bahrami. Investigating the thermal environment effects on geometrically nonlinear vibration of smart functionally graded plates. Journal of Mechanical Science and Technology, 24, (2010), pp. 775–791. https://doi.org/10.1007/s12206-010-0102-4.
[16] P. M. Phuc and N. T. Kim Khue. New finite modeling of free and forced vibration responses of piezoelectric FG plates resting on elastic foundations in thermal environments. Shock and Vibration, 2021, (2021). https://doi.org/10.1155/2021/6672370.
[17] R. A. Ahmed, B. S. Khalaf, K. M. Raheef, R. M. Fenjan, and N. M. Faleh. Investigating dynamic response of nonlocal functionally graded porous piezoelectric plates in thermal environment. Steel Compos Struct, 40, (2), (2021), pp. 243–54. https://doi.org/10.12989/scs.2021.40.2.243.
[18] W. Wang, H. Li, and L. Yao. Static bending and vibration analysis of a rectangular functionally gradient piezoelectric plate on an elastic foundation. Applied Sciences, 12, (2022). https://doi.org/10.3390/app12031517.
[19] P. T. Dat, D. V. Thom, and D. T. Luat. Free vibration of functionally graded sandwich plates with stiffeners based on the third-order shear deformation theory. Vietnam Journal of Mechanics, 38, (2016), pp. 103–122. https://doi.org/10.15625/0866-7136/38/2/6730.
[20] T. V. Lien and L. T. Ha. Dynamic analysis of functionally graded viscoelastic beams on the elastic foundation under multiple moving loads. Vietnam Journal of Mechanics, 47, (2025), pp. 90–108. https://doi.org/10.15625/0866-7136/22165.
[21] T. T. Nguyen, H. N. H. Le, V. S. Lo, and T. T. Truong. Modal analysis of plates resting on elastic foundation based on the first-order shear deformation theory and finite element method. Vietnam Journal of Mechanics, 46, (2024), pp. 354–366. -7136/21193.
[22] T. J. R. Hughes, J. A. Cottrell, and Y. Bazilevs. Isogeometric analysis: CAD, finite elements, NURBS, exact geometry and mesh refinement. Computer Methods in Applied Mechanics and Engineering, 194, (2005), pp. 4135–4195. https://doi.org/10.1016/j.cma.2004.10.008.
[23] S. Thai, H.-T. Thai, T. P. Vo, and V. I. Patel. Size-dependant behaviour of functionally graded microplates based on the modified strain gradient elasticity theory and isogeometric analysis. Computers & Structures, 190, (2017), pp. 219–241. https://doi.org/10.1016/j.compstruc.2017.05.014.
[24] C. H. Thai, A. J. M. Ferreira, and H. Nguyen-Xuan. Isogeometric analysis of sizedependent isotropic and sandwich functionally graded microplates based on modified strain gradient elasticity theory. Composite Structures, 192, (2018), pp. 274–288. https://doi.org/10.1016/j.compstruct.2018.02.060.
[25] A. Farzam and B. Hassani. Size-dependent analysis of FG microplates with temperature-dependent material properties using modified strain gradient theory and isogeometric approach. Composites Part B: Engineering, 161, (2019), pp. 150–168. https://doi.org/10.1016/j.compositesb.2018.10.028.
[26] P. T. Hung, P. Phung-Van, and C. H. Thai. A refined isogeometric plate analysis of porous metal foam microplates using modified strain gradient theory. Composite Structures, 289, (2022). https://doi.org/10.1016/j.compstruct.2022.115467.
[27] I. J. Gibson and M. F. Ashby. The mechanics of three-dimensional cellular materials. Proceedings of the Royal Society of London. A. Mathematical and Physical Sciences, 382, (1982), pp. 43–59. https://doi.org/10.1098/rspa.1982.0088.
[28] L.-L. Ke, Y.-S. Wang, J. Yang, and S. Kitipornchai. Free vibration of size-dependent magnetoelectro-elastic nanoplates based on the nonlocal theory. Acta Mechanica Sinica, 30, (2014), pp. 516–525. https://doi.org/10.1007/s10409-014-0072-3.
[29] M. R. Barati, H. Shahverdi, and A. M. Zenkour. Electro-mechanical vibration of smart piezoelectric FG plates with porosities according to a refined four-variable theory. Mechanics of Advanced Materials and Structures, 24, (2017), pp. 987–998. https://doi.org/10.1080/15376494.2016.1196799.
[30] P. T. Hung, P. Phung-Van, and C. H. Thai. A refined isogeometric plate analysis of porous metal foam microplates using modified strain gradient theory. Composite Structures, 289, (2022). https://doi.org/10.1016/j.compstruct.2022.115467.
Downloads
Published
How to Cite
License

This work is licensed under a Creative Commons Attribution-ShareAlike 4.0 International License.









