Integrating reaction-diffusion equations with a dynamic body-fitted trimmed mesh technique for level set-based structural optimization

Abstract

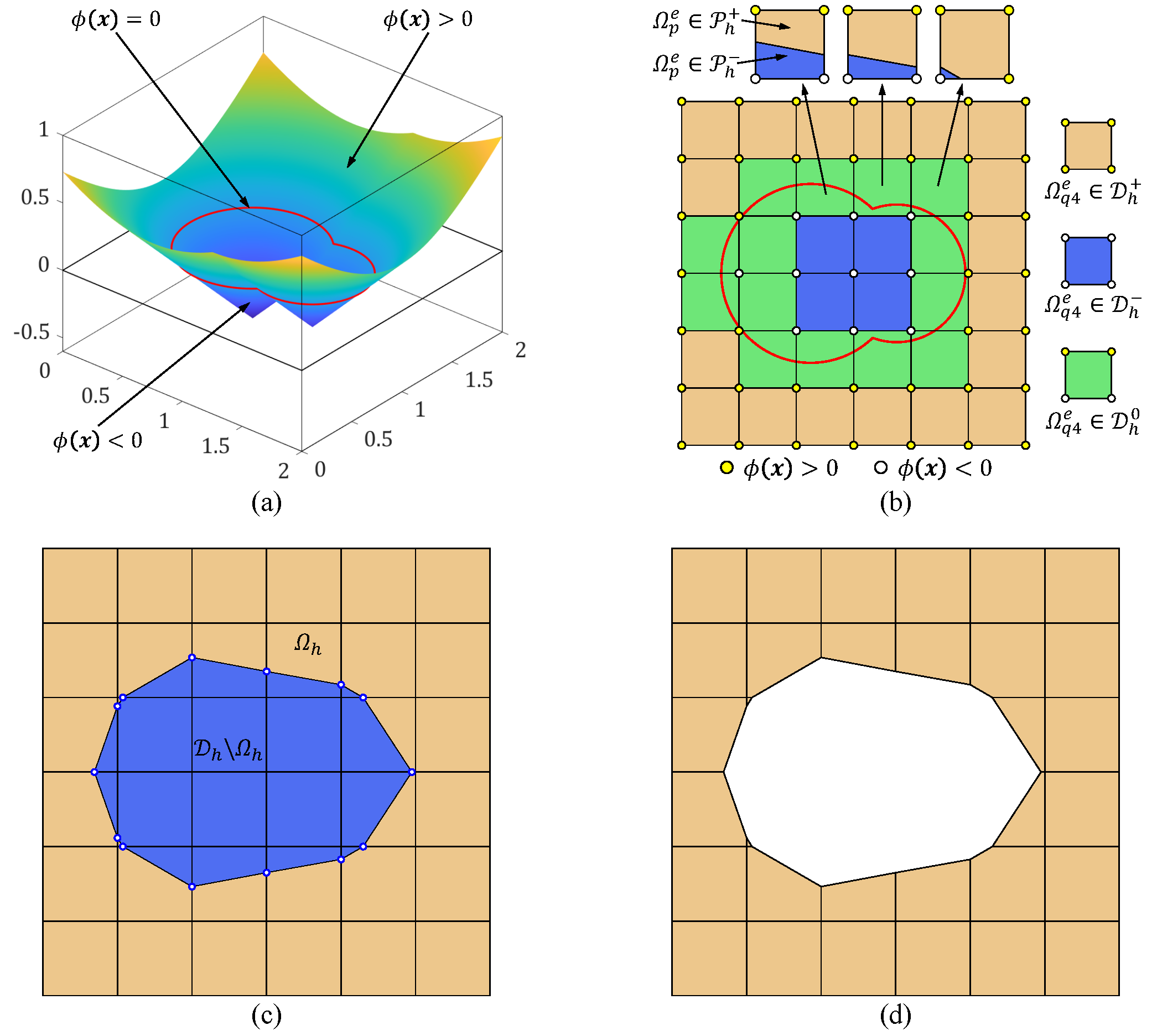
In this study, a dynamic body-fitted trimmed mesh approach is presented to address reaction-diffusion equation-based topology optimization problems, with the objective of minimizing structural compliance. The evolution of the zero-isoline of a level set function is governed by the solution of a reaction-diffusion equation, which is controlled by the topological sensitivity field and implemented on a regular background quadrilateral mesh. During each optimization iteration, a dynamic body-fitted trimmed mesh is constructed to accurately delineate the structural domain. This procedure employs the marching square algorithm, which segments the fixed background quadrilateral mesh along the zero-isoline of the level set function. To ensure precision in the optimization, the reaction-diffusion equation is solved utilizing a numerical algorithm grounded in the exact volume constraint method, which meticulously calculates the Lagrange multiplier to uphold the constraint condition. The proposed approach exhibits exceptional efficacy in solving level set-based topology optimization challenges, particularly in achieving accurate boundary representations while strictly adhering to volume constraint conditions within a predefined error tolerance. These are evident through the numerical results of two benchmark problems including 2D cantilever beam and L-bracket domain.