Forming limit prediction of advanced high-strength steels (AHSS) using an enhanced ductile damage model
Author affiliations
DOI:
https://doi.org/10.15625/0866-7136/22179Keywords:
ductile fracture, forming limit diagram, AHSS steel, ductile damage modelAbstract
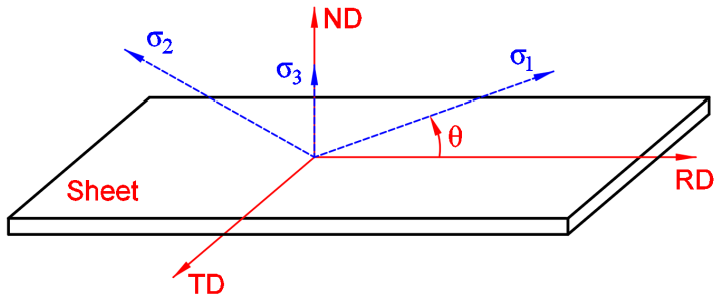
This paper presents prediction of forming limits of Advanced High-Strength Steels (AHSS) DP980 by adopting an enhanced ductile damage model to consider sheet metal anisotropy. The micro-void growth-based original damage model is transformed from principal stress space (σ1, σ2, σ3) into the equivalent stress, Lode parameter, and stress triaxiality space (σe, Lp, η). The proposed ductile fracture prediction model is then implemented and integrated with a finite element (FE) software package to conduct the deep drawing numerical simulations. The Nakajima-type specimens are adopted to predict the limiting principal plastic strains ranging from uniaxial tensile through plane-strain to biaxial tensile loading states. The forming limit diagram (FLD) of DP980 steel is established in accordance with the ISO 12004-2-2008 standard.
Downloads
References
[1] F. M. Al-Abbasi and J. A. Nemes. Micromechanical modeling of dual phase steels. International Journal of Mechanical Sciences, 45, (2003), pp. 1449–1465. https://doi.org/10.1016/j.ijmecsci.2003.10.007.
[2] A. L. Gurson. Continuum theory of ductile rupture by void nucleation and growth: Part I—yield criteria and flow rules for porous ductile media. Journal of Engineering Materials and Technology, 99, (1977), pp. 2–15. https://doi.org/10.1115/1.3443401.
[3] L. Xue. Ductile fracture modeling: theory, experimental investigation and numerical verification. PhD thesis, Massachusetts Institute of Technology, (2007).
[4] L. Xue and T. Wierzbicki. Ductile fracture initiation and propagation modeling using damage plasticity theory. Engineering Fracture Mechanics, 75, (2008), pp. 3276–3293. https://doi.org/10.1016/j.engfracmech.2007.08.012.
[5] N. Pathak, J. Adrien, C. Butcher, E. Maire, and M. Worswick. Experimental stress state-dependent void nucleation behavior for advanced high strength steels. International Journal of Mechanical Sciences, 179, (2020). https://doi.org/10.1016/j.ijmecsci.2020.105661.
[6] Z. Li, F. Shen, Y. Liu, C. Hartmann, R. Norz, S. Müntermann, W. Volk, J. Min, and J. Lian. Anisotropic fracture behavior of the 3rd generation advanced high-strength – Quenching and Partitioning steels: Experiments and simulation. Journal of Materials Research and Technology, 30, (2024), pp. 9395–9414. https://doi.org/10.2139/ssrn.4760467.
[7] N. Park, H. Huh, S. J. Lim, Y. Lou, Y. S. Kang, and M. H. Seo. Fracture-based forming limit criteria for anisotropic materials in sheet metal forming. International Journal of Plasticity, 96, (2017), pp. 1–35. https://doi.org/10.1016/j.ijplas.2016.04.014.
[8] C. Nikhare, P. D. Hodgson, and M. Weiss. Necking and fracture of advanced high strength steels. Materials Science and Engineering: A, 528, (2011), pp. 3010–3013. https://doi.org/10.1016/j.msea.2010.12.098.
[9] S. Zhang, W. Ding, K. Li, and S. Song. Prediction of ductile fracture for DP590 high-strength steel with a new semi-coupled ductile fracture criterion. Journal of the Brazilian Society of Mechanical Sciences and Engineering, 44, (2021). https://doi.org/10.1007/s40430-021-03275-z.
[10] I. U. Aydiner, B. Tatli, and T. Yalçinkaya. Investigation of failure mechanisms in dual-phase steels through cohesive zone modeling and crystal plasticity frameworks. International Journal of Plasticity, 174, (2024). https://doi.org/10.1016/j.ijplas.2024.103898.
[11] F. A. McClintock, S. M. Kaplan, and C. A. Berg. Ductile fracture by hole growth in shear bands. International Journal of Fracture, 2, (1966), pp. 614–627. https://doi.org/10.1007/bf00184558.
[12] N. L. Dung. Three-dimensional void growth in plastic materials. Mechanics Research Communications, 19, (1992), pp. 227–235. https://doi.org/10.1016/0093-6413(92)90070-q.
[13] L. Xue. Constitutive modeling of void shearing effect in ductile fracture of porous materials. Engineering Fracture Mechanics, 75, (2008), pp. 3343–3366. https://doi.org/10.1016/j.engfracmech.2007.07.022.
[14] M. Ortiz and J. C. Simo. An analysis of a new class of integration algorithms for elastoplastic constitutive relations. International Journal for Numerical Methods in Engineering, 23, (1986), pp. 353–366. https://doi.org/10.1002/nme.1620230303.
[15] K. Pack, T. Tancogne-Dejean, M. B. Gorji, and D. Mohr. Hosford-Coulomb ductile failure model for shell elements: Experimental identification and validation for DP980 steel and aluminum 6016-T4. International Journal of Solids and Structures, 151, (2018), pp. 214–232. https://doi.org/10.1016/j.ijsolstr.2018.08.006.
[16] H. H. Nguyen. Ductile damage prediction of advanced high-strength sheet steel using an enhanced crack criterion. In Proceedings of the International Conference on Sustainable Energy Technologies, Springer Nature Singapore, (2024), pp. 405–413. https://doi.org/10.1007/978- 981-97-1868-9 41.
Downloads
Published
How to Cite
License

This work is licensed under a Creative Commons Attribution-ShareAlike 4.0 International License.









