Micromechanical model to predict the effect of temperature on the behavior of unsaturated porous media
Author affiliations
DOI:
https://doi.org/10.15625/0866-7136/19023Keywords:
beam, nonlinear vibration, vibration equation, resonance oscillation, asymptotic methodAbstract
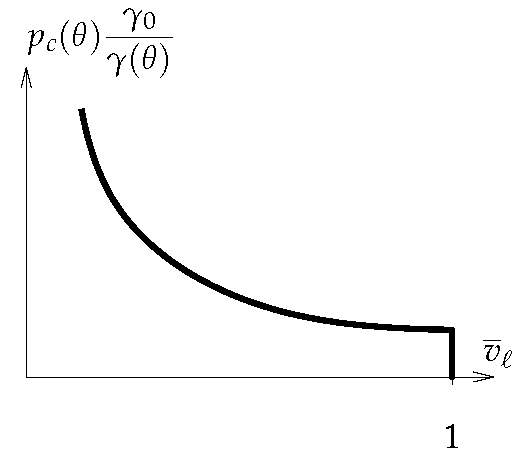
The homogenization method is used to investigate temperature effects on the water content-capillary pressure relationship and on the poro-mechanical behavior of unsaturated porous media. Two different phenomena have been considered: the temperature variations of surface tensions and the thermal dilatation of the solid phase in the framework of micromechanical models that are proposed in order to highlight the influence of the deformability of the solid phase on the macroscopic behavior. The result show that taking into account the coupling between the deformation of the porous space and the capillary effects can radically modify the prediction of the temperature influence on the capillary curve.
Downloads
Metrics
References
E. Romero, A. Gens, and A. Lloret. Temperature effects on the hydraulic behavior of an unsaturated clay. Geotechnical and Geological Engineering, 19, (3/4), (2001), pp. 311–332. DOI: https://doi.org/10.1023/A:1013133809333
P. W. Atkins. Physical chemistry. Oxford University Press, (1998).
M. Yekta-Fard and A. B. Ponter. The influences of vapor environment and temperature on the contact angle-drop size relationship. Journal of Colloid and Interface Science, 126, (1), (1988), pp. 134–140. DOI: https://doi.org/10.1016/0021-9797(88)90107-5
X. Chateau and L. Dormieux. Micromechanics of saturated and unsaturated porous media. International Journal for Numerical and Analytical Methods in Geomechanics, 26, (8), (2002), pp. 831–844. DOI: https://doi.org/10.1002/nag.227
F. A. L. Dullien. Porous media: fluid transport and pore structure. San Diego: Academic Press, 2nd edition, (1992). DOI: https://doi.org/10.1016/B978-0-12-223651-8.50007-9
X. Chateau, L. Dormieux, and Y. Xu. Évaluation de l'influence des changements de géométrie sur les déformations de séchage d'un milieu poreux fissuré. Comptes Rendus Mécanique, 331, (2003), pp. 679–686. DOI: https://doi.org/10.1016/S1631-0721(03)00146-3
L. Dormieux, D. Kondo, and F.-J. Ulm. Microporomechanics. Wiley, (2006). DOI: https://doi.org/10.1002/0470032006
B. Budiansky and R. J. O'connell. Elastic moduli of a cracked solid. International Journal of Solids and Structures, 12, (2), (1976), pp. 81–97. DOI: https://doi.org/10.1016/0020-7683(76)90044-5
O. Coussy. Mechanics of porous continua. JohnWiley & Sons, New York, NY, (1995).
X. Chateau, P. Moucheront, and O. Pitois. Micromechanics of unsaturated granular media. Journal of Engineering Mechanics, 128, (8), (2002), pp. 856–863. DOI: https://doi.org/10.1061/(ASCE)0733-9399(2002)128:8(856)
B. V. Tran. Approche micromécanique du comportement d’un matériau fissuré non saturé. PhD thesis, Université Paris-Est, (2010).
Downloads
Published
How to Cite
License
This work is licensed under a Creative Commons Attribution-ShareAlike 4.0 International License.
