A single degree of freedom model for cracked beam
Author affiliations
DOI:
https://doi.org/10.15625/0866-7136/18464Keywords:
cracked beam, simplified model, frequency response function, frequency domain assurance criterionAbstract
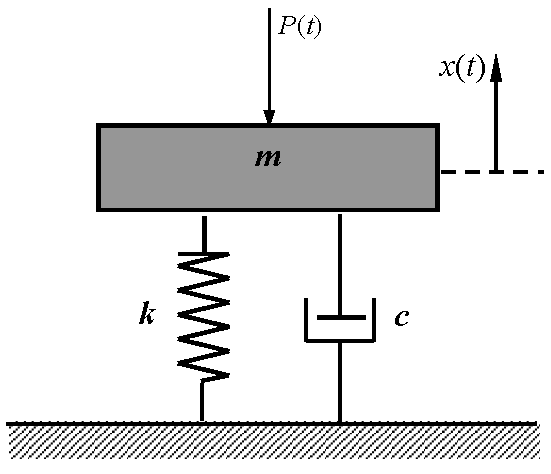
This paper presents a simplified model of cracked beam by single-degree-of-freedom system. Equivalence between the beam and SDOF models means that they have the same fundamental natural frequency and similar frequency response functions (FRFs). Similarity of FRFs is checked by using the frequency-domain assurance criterion acknowledged herein as spectral similarity index (SSI). Finally, FRFs of both the cracked beam and its simplified SDOF model have been examined versus crack location and depth using the so-called spectral damage index (SDI). Numerical results show that SDI is significantly sensitive to crack and could be used as a novel indicator for crack detection in beam by measurements of frequency response functions.
Downloads
Metrics
References
N. T. Khiem. Fundamentals of structural dynamics. VNU Publishing House, Hanoi, (2004). (in Vietnamese).
T. Irvine. An introduction to shock and vibration response spectra, Revision A. Vibrationdata Publications, (2019).
N. T. Khiem and T. T. Hai. Vibration in engineering. VNU Publishing House, Hanoi, (2020). (in Vietnamese).
U. Andreaus, L. Placidi, and G. Rega. Soft impact dynamics of a cantilever beam: equivalent SDOF model versus infinite-dimensional system. Proceedings of the Institution of Mechanical Engineers, Part C: Journal of Mechanical Engineering Science, 225, (2011), pp. 2444–2456. DOI: https://doi.org/10.1177/0954406211414484
U. K. Pandey and G. S. Benipal. Response of SDOF bilinear elasto-dynamical models of cracked concrete beams for El Centro earthquake. The IES Journal Part A: Civil & Structural Engineering, 6, (2013), pp. 222–238. DOI: https://doi.org/10.1080/19373260.2013.801146
M. Rezaee and H. Fekrmandi. A theoretical and experimental investigation on free vibration vehavior of a cantilever beam with a breathing crack. Shock and Vibration, 19, (2), (2012), pp. 175–186. DOI: https://doi.org/10.1155/2012/563916
F. Stochino and G. Carta. SDOF models for reinforced concrete beams under impulsive loads accounting for strain rate effects. Nuclear Engineering and Design, 276, (2014), pp. 74–86. DOI: https://doi.org/10.1016/j.nucengdes.2014.05.022
M. Mousavi, D. Holloway, and J. C. Olivier. Using a moving load to simultaneously detect location and severity of damage in a simply supported beam. Journal of Vibration and Control, 25, (2019), pp. 2108–2123. DOI: https://doi.org/10.1177/1077546319849772
R. J. Allemang. The modal assurance criterion–twenty years of use and abuse. Sound and Vibration, 37, (8), (2003), pp. 14–23.
R. P. C. Sampaio, N. M. M. Maia, and J. M. M. Silva. The frequency domain assurance criterion as a tool for damage detection. Key Engineering Materials, 245-246, (2003), pp. 69–76. DOI: https://doi.org/10.4028/www.scientific.net/KEM.245-246.69
N. T. Khiem. Vibrations of cracked functionally graded beams: General solution and application – A review. Vietnam Journal of Mechanics, 44, (2022), pp. 317–347. DOI: https://doi.org/10.15625/0866-7136/17986
V. B. Zaalishvili and I. D. Muzaeb. One effective method for solving initial-boundary problems of transverse vibrations of a beam, taking into account its internal resistance. Geology and Geophysics of Russian South, 13, (2023), pp. 55–66. DOI: https://doi.org/10.46698/VNC.2023.63.12.005
Downloads
Published
How to Cite
License
This work is licensed under a Creative Commons Attribution-ShareAlike 4.0 International License.
Funding data
-
Trường Đại học Công nghệ, Đại học Quốc Gia Hà Nội
Grant numbers CN22.13
