Free vibration analysis of FGM framed nanostructures using variational-consistent boundary conditions
Author affiliations
DOI:
https://doi.org/10.15625/0866-7136/18192Keywords:
FGM, nanobeam, DSM, variational-consistent boundary conditions, nondimensional frequencyAbstract
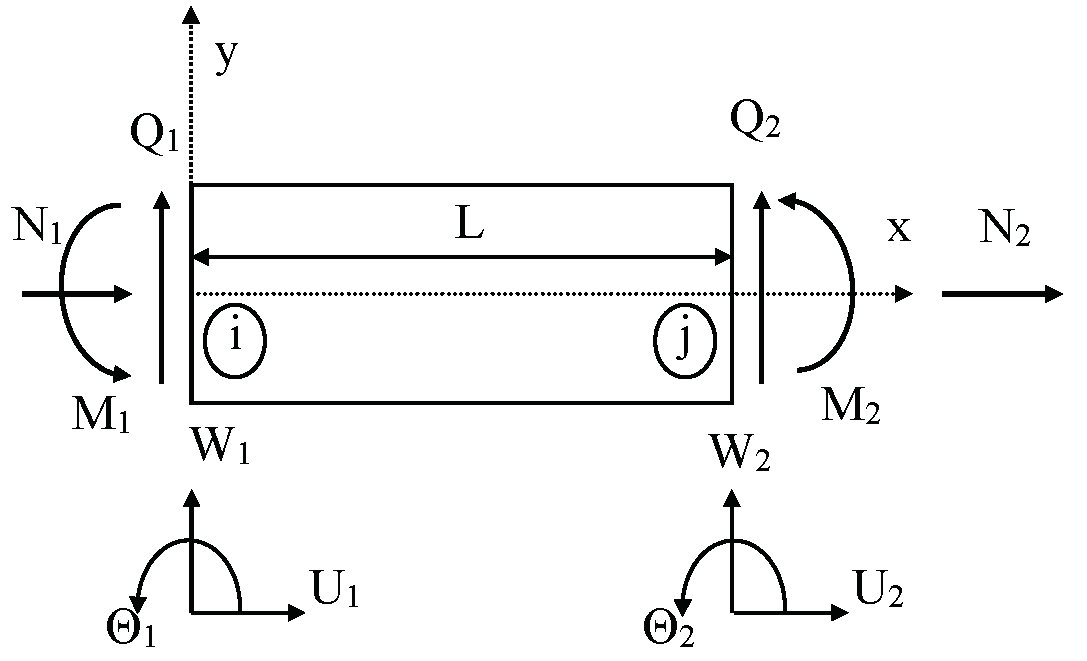
This paper analyses free vibrations of framed nanostructures made of Functionally Graded Material (FGM) based on the Nonlocal Elastic Theory (NET) and the Dynamic Stiffness Method (DSM). FGM characteristics vary nonlinearly throughout the height of the beam element. The NET considers the nonlocal parameter that perfectly captured the size effect of nanostructures. However, the NET makes nonlocal paradoxes in the bending and vibration behaviour of framed nanostructures with the free ends. To overcome these phenomena, the nanostructure is modelled according to the Euler–Bernoulli beam theory and the variational-consistent nonlocal boundary conditions have been derived. The exact solutions of differential equations of motion and variational-consistent nonlocal boundary conditions are found using the DSM. The influences of the nonlocal, material, geometry parameters and Pasternak’s foundation on the free vibration are then analyzed. It is shown that the study can be applied to other FGMs as well as more complicated framed structures.
Downloads
References
H.-S. Shen. Functionally graded materials: nonlinear analysis of plates and shells. CRC Press, (2016).
M. H. Ghayesh and A. Farajpour. A review on the mechanics of functionally graded nanoscale and microscale structures. International Journal of Engineering Science, 137, (2019), pp. 8–36.
A. Farajpour, M. H. Ghayesh, and H. Farokhi. A review on the mechanics of nanostructures. International Journal of Engineering Science, 133, (2018), pp. 231–263.
M. A. Roudbari, T. D. Jorshari, C. Lü, R. Ansari, A. Z. Kouzani, and M. Amabili. A review of size-dependent continuum mechanics models for micro- and nano-structures. Thin-Walled Structures, 170, (2022).
V. S. Chandel, G. Wang, and M. Talha. Advances in modelling and analysis of nano structures: a review. Nanotechnology Reviews, 9, (2020), pp. 230–258.
A. Garg, H. D. Chalak, A. M. Zenkour, M.-O. Belarbi, and M.-S.-A. Houari. A review of available theories and methodologies for the analysis of nano isotropic, nano functionally graded, and CNT reinforced nanocomposite structures. Archives of Computational Methods in Engineering, 29, (2022), pp. 2237–2270.
A. C. Eringen. Nonlocal continuum field theories. Springer Science & Business Media, New York, US, (2002).
C. Polizzotto. Nonlocal elasticity and related variational principles. International Journal of Solids and Structures, 38, (2001), pp. 7359–7380.
M. A. Eltaher, M. E. Khater, and S. A. Emam. A review on nonlocal elastic models for bending, buckling, vibrations, and wave propagation of nanoscale beams. Applied Mathematical Modelling, 40, (2016), pp. 4109–4128.
H. Salehipour, A. R. Shahidi, and H. Nahvi. Modified nonlocal elasticity theory for functionally graded materials. International Journal of Engineering Science, 90, (2015), pp. 44–57.
J. N. Reddy. Nonlocal theories for bending, buckling and vibration of beams. International Journal of Engineering Science, 45, (2007), pp. 288–307.
C. M. Wang, Y. Y. Zhang, and X. Q. He. Vibration of nonlocal Timoshenko beams. Nanotechnology, 18, (2007).
C. Li, C. W. Lim, J. L. Yu, and Q. C. Zeng. Analytical solutions for vibration of simply supported nonlocal nanobeams with an axial force. International Journal of Structural Stability and Dynamics, 11, (2011), pp. 257–271.
M. ¸Sim¸sek and H. H. Yurtcu. Analytical solutions for bending and buckling of functionally graded nanobeams based on the nonlocal Timoshenko beam theory. Composite Structures, 97, (2013), pp. 378–386.
O. Rahmani and O. Pedram. Analysis and modeling the size effect on vibration of functionally graded nanobeams based on nonlocal Timoshenko beam theory. International Journal of Engineering Science, 77, (2014), pp. 55–70.
I. Mechab, N. E. Meiche, and F. Bernard. Free vibration analysis of higher-order shear elasticity nanocomposite beams with consideration of nonlocal elasticity and poisson effect. Journal of Nanomechanics and Micromechanics, 6, (2016).
B. Uymaz. Forced vibration analysis of functionally graded beams using nonlocal elasticity. Composite Structures, 105, (2013), pp. 227–239.
M. A. Eltaher, A. E. Alshorbagy, and F. F. Mahmoud. Vibration analysis of Euler–Bernoulli nanobeams by using finite element method. Applied Mathematical Modelling, 37, (2013), pp. 4787–4797.
M. A. Eltaher, F. F. Mahmoud, A. E. Assie, and E. I. Meletis. Coupling effects of nonlocal and surface energy on vibration analysis of nanobeams. Applied Mathematics and Computation, 224, (2013), pp. 760–774.
S. Adhikari, T. Murmu, and M. A. McCarthy. Dynamic finite element analysis of axially vibrating nonlocal rods. Finite Elements in Analysis and Design, 63, (2013), pp. 42–50.
S. C. Pradhan. Nonlocal finite element analysis and small scale effects of CNTs with Timoshenko beam theory. Finite Elements in Analysis and Design, 50, (2012), pp. 8–20.
M. A. Eltaher, A. E. Alshorbagy, and F. F. Mahmoud. Determination of neutral axis position and its effect on natural frequencies of functionally graded macro/nanobeams. Composite Structures, 99, (2013), pp. 193–201.
M. A. Eltaher, S. A. Emam, and F. F. Mahmoud. Free vibration analysis of functionally graded size-dependent nanobeams. Applied Mathematics and Computation, 218, (2012), pp. 7406–7420.
M. A. Eltaher, A. A. Abdelrahman, A. Al-Nabawy, M. Khater, and A. Mansour. Vibration of nonlinear graduation of nano-Timoshenko beam considering the neutral axis position. Applied Mathematics and Computation, 235, (2014), pp. 512–529.
M. A. Eltaher, A. Khairy, A. M. Sadoun, and F.-A. Omar. Static and buckling analysis of functionally graded Timoshenko nanobeams. Applied Mathematics and Computation, 229, (2014), pp. 283–295.
A. I. Aria and M. I. Friswell. A nonlocal finite element model for buckling and vibration of functionally graded nanobeams. Composites Part B: Engineering, 166, (2019), pp. 233–246.
F. Ebrahimi and P. Nasirzadeh. A nonlocal Timoshenko beam theory for vibration analysis of thick nanobeams using differential transform method. Journal of Theoretical and Applied Mechanics, (2015).
S. K. Jena and S. Chakraverty. Free vibration analysis of variable cross-section single-layered graphene nano-ribbons (SLGNRs) using differential quadrature method. Frontiers in Built Environment, 4, (2018).
O. C. Zienkiewicz, R. L. Taylor, and J. Z. Zhu. The finite element method: its basis and fundamentals. Elsevier, (2005).
E. Oñate. Structural analysis with the finite element method. Linear statics: volume 2: beams, plates and shells. Springer Science & Business Media, (2013).
H. Su and J. R. Banerjee. Development of dynamic stiffness method for free vibration of functionally graded Timoshenko beams. Computers & Structures, 147, (2015), pp. 107–116.
T. V. Lien, N. T. Duc, and N. T. Khiem. Free and forced vibration analysis of multiple cracked FGM multi span continuous beams using dynamic stiffness method. Latin American Journal of Solids and Structures, 16, (2019).
A. Y. T. Leung. Dynamic stiffness and substructures. Springer Science & Business Media, (2012).
J. R. Banerjee. Review of the dynamic stiffness method for free-vibration analysis of beams. Transportation Safety and Environment, 1, (2019), pp. 106–116.
D. Karličić, T. Murmu, S. Adhikari, and M. McCarthy. Non-local structural mechanics. John Wiley & Sons, Inc, (2015).
S. Adhikari, T. Murmu, and M. A. McCarthy. Frequency domain analysis of nonlocal rods embedded in an elastic medium. Physica E: Low-dimensional Systems and Nanostructures, 59, (2014), pp. 33–40.
S. Adhikari, D. Karličić, and X. Liu. Dynamic stiffness of nonlocal damped nanobeams on elastic foundation. European Journal of Mechanics - A/Solids, 86, (2021).
M. S. Taima, T. A. El-Sayed, and S. H. Farghaly. Free vibration analysis of multistepped nonlocal Bernoulli–Euler beams using dynamic stiffness matrix method. Journal of Vibration and Control, 27, (2020), pp. 774–789.
J. Peddieson, G. R. Buchanan, and R. P. McNitt. Application of nonlocal continuum models to nanotechnology. International Journal of Engineering Science, 41, (2003), pp. 305–312.
E. Ghavanloo, H. Rafii-Tabar, and S. A. Fazelzadeh. Computational continuum mechanics of nanoscopic structures. Springer International Publishing, (2019).
S. Ceballes, K. Larkin, E. Rojas, S. S. Ghaffari, and A. Abdelkefi. Nonlocal elasticity and boundary condition paradoxes: a review. Journal of Nanoparticle Research, 23, (2021).
N. Challamel, Z. Zhang, C. M. Wang, J. N. Reddy, Q. Wang, T. Michelitsch, and B. Collet. On nonconservativeness of Eringen’s nonlocal elasticity in beam mechanics: correction from a discrete-based approach. Archive of Applied Mechanics, 84, (2014), pp. 1275–1292.
P. Khodabakhshi and J. N. Reddy. A unified integro-differential nonlocal model. International Journal of Engineering Science, 95, (2015), pp. 60–75.
Z. Zhang, N. Challamel, and C. M. Wang. Eringen's small length scale coefficient for buckling of nonlocal Timoshenko beam based on microstructured beam model. Journal of Applied Physics, 114, (2013).
J. W. Yan, L. H. Tong, C. Li, Y. Zhu, and Z. W. Wang. Exact solutions of bending deflections for nano-beams and nano-plates based on nonlocal elasticity theory. Composite Structures, 125, (2015), pp. 304–313.
X.-J. Xu, Z.-C. Deng, K. Zhang, and W. Xu. Observations of the softening phenomena in the nonlocal cantilever beams. Composite Structures, 145, (2016), pp. 43–57.
L. V. Tran, D. B. Tran, and P. T. T. Phan. Free vibration analysis of stepped FGM nanobeams using nonlocal dynamic stiffness model. Journal of Low Frequency Noise, Vibration and Active Control, (2023).
Downloads
Published
How to Cite
License

This work is licensed under a Creative Commons Attribution-ShareAlike 4.0 International License.
Funding data
-
Tru?ng Ð?i h?c Xây d?ng
Grant numbers 32-2022/KHXD-TĐ









