Some approximate buckling solutions of triple-walled carbon nanotube
Author affiliations
DOI:
https://doi.org/10.15625/0866-7136/17054Keywords:
triple-walled carbon nanotube, Bubnov─Galerkin method, Petrov─Galerkin method, buckling loadAbstract
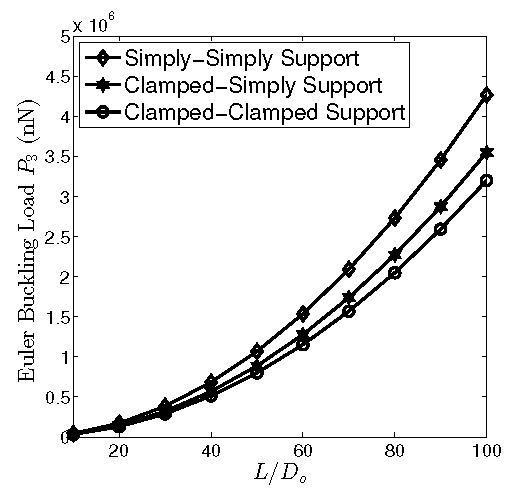
The present investigation analyses the critical buckling studies of triple-walled carbon nanotube using the Euler─Bernoulli model. The present study deals with three different boundary conditions, namely, simply-simply, clamped-clamped, and clamped-simply supported carbon nanotube. Using Bubnov─Galerkin and Petrov─Galerkin methods, the continuum model estimates the critical buckling load. The main advantage of these two approximate methods is to obtain a quick and valid result. The first and second Euler critical buckling loads decrease with the increase of length to outer diameter ratio for boundary conditions like simply-simply, clamped-clamped, and clamped-simply supported. Interestingly, the increase in the length to outer diameter ratio results in the rise in third Euler critical buckling for all three different boundary conditions. These two approximate methods provide reliable buckling load estimation using suitable polynomials.
Downloads
Metrics
References
S. Iijima. Helical microtubules of graphitic carbon. Nature, 354, (6348), (1991), pp. 56–58. DOI: https://doi.org/10.1038/354056a0
V. Senthilkumar. Axial vibration of double-walled carbon nanotubes using double-nanorod model with van der Waals force under Pasternak medium and magnetic effects. Vietnam Journal of Mechanics, 44, (1), (2022), pp. 29–43. DOI: https://doi.org/10.15625/0866-7136/16582
G. Dresselhaus, M. S. Dresselhaus, and R. Saito. Physical properties of carbon nanotubes. World Scientific, (1998). DOI: https://doi.org/10.1088/2058-7058/11/1/32
A. Eatemadi, H. Daraee, H. Karimkhanloo, M. Kouhi, N. Zarghami, A. Akbarzadeh, M. Abasi, Y. Hanifehpour, and S. W. Sang. Carbon nanotubes: properties, synthesis, purification, and medical applications. Nanoscale Research Letters, 9, (1), (2014), pp. 1–13. DOI: https://doi.org/10.1186/1556-276X-9-393
C. M. Wang and C. Y. Wang. Exact solutions for buckling of structural members. CRC Press, (2004). DOI: https://doi.org/10.1201/9780203483534
C. M. Wang, Y. Y. Zhang, Y. Xiang, and J. N. Reddy. Recent studies on buckling of carbon nanotubes. Applied Mechanics Reviews, 63, (3), (2010), pp. 030804–030821. DOI: https://doi.org/10.1115/1.4001936
R. C. Batra and A. Sears. Continuum models of multi-walled carbon nanotubes. International Journal of Solids and Structures, 44, (22-23), (2007), pp. 7577–7596. DOI: https://doi.org/10.1016/j.ijsolstr.2007.04.029
C. C. Hwang, Y. C. Wang, Q. Y. Kuo, and J. M. Lu. Molecular dynamics study of multi-walled carbon nanotubes under uniaxial loading. Physica E: Low-dimensional Systems and Nanostructures, 42, (4), (2010), pp. 775–778. DOI: https://doi.org/10.1016/j.physe.2009.10.064
M. Nishimura, Y. Takagi, and M. Arai. Molecular dynamics study on buckling behavior of non-defective and defective triple-walled carbon nanotubes. Journal of Solid Mechanics and Materials Engineering, 7, (3), (2013), pp. 403–416. DOI: https://doi.org/10.1299/jmmp.7.403
I. Elishakoff and D. Pentaras. Buckling of a double-walled carbon nanotube. Advanced Science Letters, 2, (3), (2009), pp. 372–376. DOI: https://doi.org/10.1166/asl.2009.1061
S. Kitipornchai, X. Q. He, and K. M. Liew. Buckling analysis of triple-walled carbon nanotubes embedded in an elastic matrix. Journal of Applied Physics, 97, (11), (2005), pp. 114318–114324. DOI: https://doi.org/10.1063/1.1925334
X. Guo, A. Y. T. Leung, H. Jiang, X. Q. He, and Y. Huang. Critical strain of carbon nanotubes: an atomic-scale finite element study. Journal of Applied Mechanics, 74, (2), (2007), pp. 347–351. DOI: https://doi.org/10.1115/1.2198548
J. Lu, C. Hwang, Q. Kuo, and Y. Wang. Mechanical buckling of multi-walled carbon nanotubes: The effects of slenderness ratio. Physica E: Low-dimensional Systems and Nanostructures, 40, (5), (2008), pp. 1305–1308. DOI: https://doi.org/10.1016/j.physe.2007.08.120
R. Rahmani and M. Antonov. Axial and torsional buckling analysis of single-and multiwalled carbon nanotubes: finite element comparison between armchair and zigzag types. SN Applied Sciences, 1, (9), (2019), pp. 1–13. DOI: https://doi.org/10.1007/s42452-019-1190-0
S. B. Coşkun. Advances in computational stability analysis. InTech, (2012). DOI: https://doi.org/10.5772/3085
D. Pentaras and I. Elishakoff. Free vibration of triple-walled carbon nanotubes. Acta Mechanica, 221, (3), (2011), pp. 239–249. DOI: https://doi.org/10.1007/s00707-011-0496-9
C. Q. Ru. Column buckling of multiwalled carbon nanotubes with interlayer radial displacements. Physical Review B, 62, (24), (2000), pp. 16962–16967. DOI: https://doi.org/10.1103/PhysRevB.62.16962
C. Q. Ru. Effect of van der Waals forces on axial buckling of a double-walled carbon nanotube. Journal of Applied Physics, 87, (10), (2000), pp. 7227–7237. DOI: https://doi.org/10.1063/1.372973
C. Q. Ru. Axially compressed buckling of a doublewalled carbon nanotube embedded in an elastic medium. Journal of the Mechanics and Physics of Solids, 49, (6), (2001), pp. 1265–1279. DOI: https://doi.org/10.1016/S0022-5096(00)00079-X
V. Senthilkumar. Buckling analysis of a single-walled carbon nanotube with nonlocal continuum elasticity by using differential transform method. Advanced Science Letters, 3, (3), (2010), pp. 337–340. DOI: https://doi.org/10.1166/asl.2010.1131
M. Malikan, V. A. Eremeyev, and H. M. Sedighi. Buckling analysis of a non-concentric double-walled carbon nanotube. Acta Mechanica, 231, (12), (2020), pp. 5007–5020. DOI: https://doi.org/10.1007/s00707-020-02784-7
I. Elishakoff, K. Dujat, G. Muscolino, S. Bucas, T. Natsuki, C. M. Wang, D. Pentaras, C. Versaci, J. Storch, N. Challamel, Y. Zhang, and G. Ghyselinck. Carbon nanotubes and nanosensors: Vibration, buckling and balistic impact. John Wiley & Sons, (2013). DOI: https://doi.org/10.1002/9781118562000
I. Elishakoff, K. Dujat, and M. Lemaire. Buckling of double-walled carbon nanotube. Vietnam Journal of Mechanics, 34, (4), (2012), pp. 217–224. DOI: https://doi.org/10.15625/0866-7136/34/4/2572
H. Shima. Buckling of carbon nanotubes: a state of the art review. Materials, 5, (1), (2011), pp. 47–84. DOI: https://doi.org/10.3390/ma5010047
E. Bekyarova, Y. Ni, E. B. Malarkey, V. Montana, J. L. McWilliams, R. C. Haddon, and V. Parpura. Applications of carbon nanotubes in biotechnology and biomedicine. Journal of Biomedical Nanotechnology, 1, (1), (2005), pp. 3–17. DOI: https://doi.org/10.1166/jbn.2005.004
L. Qin. Determination of the chiral indices (n,m) of carbon nanotubes by electron diffraction. Physical Chemistry Chemical Physics, 9, (1), (2007), pp. 31–48. DOI: https://doi.org/10.1039/B614121H
M. Noureddine, L. Mohamed, Y. Al-Douri, B. Djillali, and B. Mokhtar. Effect of chiral angle and chiral index on the vibration of single-walled carbon nanotubes using nonlocal Euler-Bernoulli beam model. Computational Condensed Matter, 30, (2022). DOI: https://doi.org/10.1016/j.cocom.2022.e00655
S. Gopalakrishnan and S. Narendar. Wave propagation in nanostructures: Nonlocal continuum mechanics formulations. Springer Science & Business Media, (2013). DOI: https://doi.org/10.1007/978-3-319-01032-8
A. Sears and R. C. Batra. Macroscopic properties of carbon nanotubes from molecular-mechanics simulations. Physical Review B, 69, (23), (2004), pp. 235406–235415. DOI: https://doi.org/10.1103/PhysRevB.69.235406
Downloads
Published
How to Cite
Issue
Section
License
This work is licensed under a Creative Commons Attribution-ShareAlike 4.0 International License.
