Buckling of chiral elastic rings spanned by fluid films
Author affiliations
DOI:
https://doi.org/10.15625/0866-7136/16726Keywords:
buckling, elastic ring, chirality, cosseratsserat rod, fluid filmAbstract
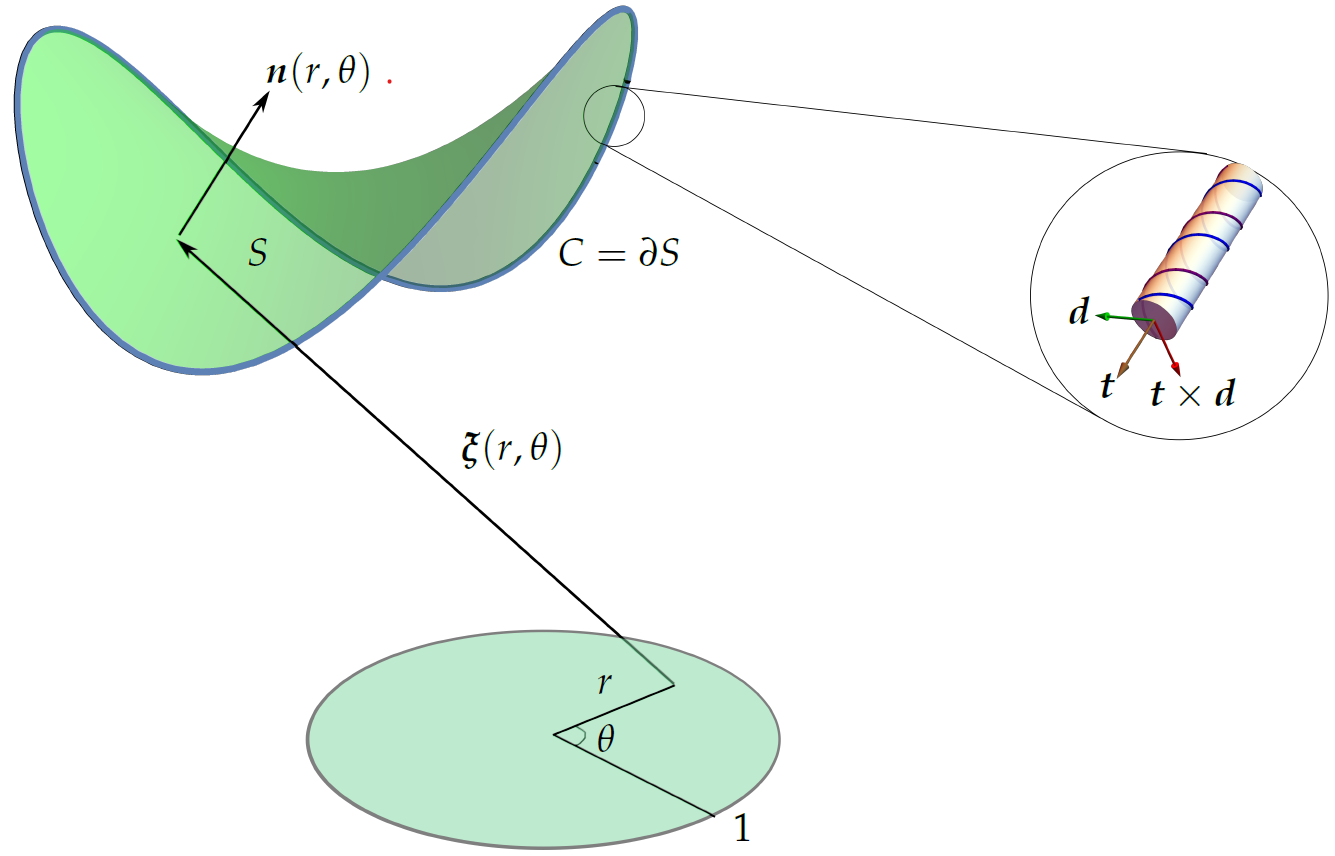
We use variational method to examine buckling of chiral elastic rings spanned by fluid films. We find that the critical surface tension of the fluid film at which buckling occurs depends on the degree of chirality, regardless whether the ring possesses left-handed chirality or right-handed chirality. Additionally, the chirality always has a destabilizing effect on buckling, yielding to buckle at a critical surface tension smaller than that of the achiral elastic rings. The destabilizing effect of chirality, however, can be reduced by increasing the twisting rigidity to bending rigidity of filaments (twist-to-bend ratio).
Downloads
Metrics
References
M. M. Lévy. Mémoire sur un nouveau cas intégrable du probléme de l’élastique et lune de ses applications. Journal of Pure and Applied Mathematics, 10, (1884), pp. 5–42.
R. Hashemi and R. Avazmohammadi. Surface effects on stability of nanorings under uniform pressure. Journal of Applied Physics, 114, (2013). DOI: https://doi.org/10.1063/1.4824818
D. F. Windenburg and C. Trilling. Collapse by instability of thin cylindrical shells under external pressure. Transactions of the American Society of Mechanical Engineers, 56, (11), (1934), pp. 819–825.
T. Savin, N. A. Kurpios, A. E. Shyer, P. Florescu, H. Liang, L. Mahadevan, and C. J. Tabin. On the growth and form of the gut. Nature, 476, (7358), (2011), pp. 57–62. DOI: https://doi.org/10.1038/nature10277
A. Catte, J. C. Patterson, M. K. Jones, W. G. Jerome, D. Bashtovyy, Z. Su, F. Gu, J. Chen, M. P. Aliste, S. C. Harvey, L. Li, G. Weinstein, and J. P. Segrest. Novel Changes in Discoidal High Density Lipoprotein Morphology: A Molecular Dynamics Study. Biophysical Journal, 90, (12), (2006), pp. 4345 –4360. DOI: https://doi.org/10.1529/biophysj.105.071456
J. Plateau. Récherches expérimentales et théoriques sur les figures d’équilibre d’une masse liquide sans pesanteur, Septième série. Mémoires de l’Académie royale des sciences, des lettres et des beaux-arts de Belgique, Classe des sciences, XXXVI, (1866), pp. 1–66.
F. Bernatzki and R. Ye. Minimal surfaces with an elastic boundary. Annals of Global Analysis and Geometry, 19, (2001), pp. 1–9. DOI: https://doi.org/10.1023/A:1006734619701
L. Giomi and L. Mahadevan. Minimal surfaces bounded by elastic lines. Proceedings of the Royal Society of London Series A, Mathematical, Physical and Engineering Sciences, 468, (2012), pp. 1851–1864. DOI: https://doi.org/10.1098/rspa.2011.0627
Y.-C. Chen and E. Fried. Stability and bifurcation of a soap film spanning a flexible loop. Journal of Elasticity, 116, (1), (2014), pp. 75–100. DOI: https://doi.org/10.1007/s10659-013-9458-x
A. Biria and E. Fried. Buckling of a soap film spanning a flexible loop resistant to bending and twisting. Proceedings of the Royal Society of London Series A, Mathematical, Physical and Engineering Sciences, 470, (2014), pp. 1–17. DOI: https://doi.org/10.1098/rspa.2014.0368
A. Biria and E. Fried. Theoretical and experimental study of the stability of a soap film spanning a flexible loop. International Journal of Engineering Science, 94, (2015), pp. 86–102. DOI: https://doi.org/10.1016/j.ijengsci.2015.05.002
G. Giusteri, P. Franceschini, and E. Fried. Instability paths in the Kirchhoff–Plateau problem. Journal of Nonlinear Science, 26, (4), (2016), pp. 1097–1132. DOI: https://doi.org/10.1007/s00332-016-9299-4
T. M. Hoang and E. Fried. Influence of a spanning liquid film on the stability and buckling of a circular loop with intrinsic curvature or intrinsic twist density. Mathematics and Mechanics of Solids, 23, (1), (2018), pp. 43–66. DOI: https://doi.org/10.1177/1081286516666135
P. N. R. D. Kamien, T. C. Lubensky and C. S. O’Hern. Direct determination of DNA twist-stretch coupling. Europhys. Lett., 38, (3), (1997), pp. 237–242. DOI: https://doi.org/10.1209/epl/i1997-00231-y
J. D. Moroz and P. Nelson. Torsional directed walks, entropic elasticity, and DNA twist stiffness. Proc. Natl. Acad. Sci. USA, 94, (1997), pp. 14418–14422. DOI: https://doi.org/10.1073/pnas.94.26.14418
B. Đuričković, A. Goriely, and J. H. Maddocks. Twist and stretch of helices explained via the Kirchhoff-Love rod model of elastic filaments. Physical Review Letters, 111, (2013). DOI: https://doi.org/10.1103/PhysRevLett.111.108103
J. F. Marko and E. D. Sigga. Bending and twisting elasticity of DNA. Macromolecules, 27, (1994), pp. 981–988. DOI: https://doi.org/10.1021/ma00082a015
J. F. Marko. Stretching must twist DNA. Europhys. Lett., 38, (3), (1997), pp. 183–188. DOI: https://doi.org/10.1209/epl/i1997-00223-5
T. M. Hoang. Influence of chirality on buckling and initial postbuckling of inextensible rings subject to central loadings. International Journal of Solids and Structures, 172-173, (2019), pp. 97–109. DOI: https://doi.org/10.1016/j.ijsolstr.2019.03.029
T. M. Hoang. Postbuckling of chiral elastic rings with intrinsic twist. International Journal of Solids and Structures, 225, (2021). DOI: https://doi.org/10.1016/j.ijsolstr.2021.03.020
S. S. Antman. Nonlinear Problems of Elasticity. Springer, (1995). DOI: https://doi.org/10.1007/978-1-4757-4147-6
A. Goriely. Twisted elastic rings and the rediscoveries of Michell’s instability. Journal of Elasticity, 84, (3), (2006), pp. 281–299. DOI: https://doi.org/10.1007/s10659-006-9055-3
Downloads
Published
How to Cite
Issue
Section
License
This work is licensed under a Creative Commons Attribution-ShareAlike 4.0 International License.
